|
|
|
|
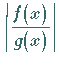 über alle Grenzen
wachsen.
über alle Grenzen
wachsen.
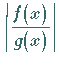 beim Grenzübergang
beim Grenzübergang 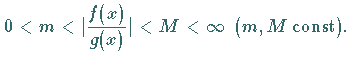
| (2.27a) |
| (2.27b) |
| Beispiel A | |
|
| |
| Beispiel B | |
|
| |
| Beispiel C | |
|
| |
5. Polynome:
Die Größenordnung von ganzrationalen Funktionen kann durch den Grad der Funktion
ausgedrückt werden.
So hat die Funktion ![]() die Größenordnung
die Größenordnung ![]() ,
ein Polynom mit dem Grad
,
ein Polynom mit dem Grad ![]() hat eine um
hat eine um ![]() höhere Ordnung als ein Polynom mit dem Grad
höhere Ordnung als ein Polynom mit dem Grad ![]() .
Allerdings gilt diese Regel nicht für alle elementaren Funktionen.
.
Allerdings gilt diese Regel nicht für alle elementaren Funktionen.
6. Exponentialfunktion:
Die Exponentialfunktion wird stärker unendlich als jede noch so hohe Potenz ![]() (
(![]() feste natürliche Zahl):
feste natürliche Zahl):
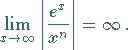 |
(2.28a) |
| (2.28b) |
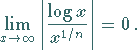 |
(2.29) |
|
|
|