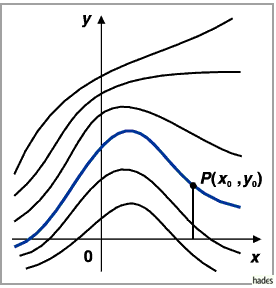
Richtungsfeld, Vertikale Richtungen
1. Richtungsfeld:
Wenn durch den Punkt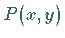 
die Kurve einer Lösung 
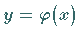der Differentialgleichung 
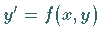geht, dann kann der Richtungsfaktor 
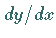der
Tangente an die Kurve in diesem Punkt unmittelbar aus der Differentialgleichung bestimmt
werden.
Damit definiert die Differentialgleichung in jedem Punkt die Richtung der Tangente an eine
Lösungskurve.
Die Gesamtheit dieser Richtungen bildet das Richtungsfeld (s. Abbildung).
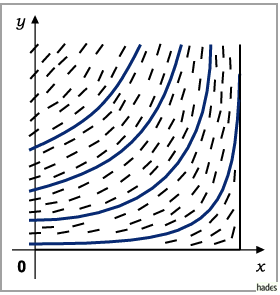
Als Element des Richtungsfeldes bezeichnet man einen Punkt zusammen mit der in ihm
gegebenen Richtung.
Geometrisch betrachtet bedeutet die Integration einer Differentialgleichung 1. Ordnung
somit die Verbindung der Elemente des Richtungsfeldes zu Integralkurven , deren
Tangenten in jedem Punkt eine Richtung besitzen, die mit der des Richtungsfeldes in dem
betreffenden Punkt übereinstimmt.
2. Vertikale Richtungen:
Wenn in einem Feld vertikale Richtungen auftreten, d.h. wenn die Funktion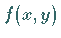 
einen
Pol besitzt, vertauscht man die Rolle der abhängigen und unabhängigen Variablen und
faßt die Differentialgleichung
 |
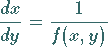(9.4) |
als äquivalent zur vorgegebenen Differentialgleichung (9.2) auf.
In den Gebieten, in denen die Bedingungen des Existenzsatzes für die
Differentialgleichungen (9.2) oder (9.4)
erfüllt sind, geht durch jeden Punkt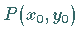 
eine eindeutig bestimmte Integralkurve
(s. Abbildung).
