Themen dieser Seite
Existenz einer Lösung
Zurückführung auf ein System von Differentialgleichungen:
Jede explizite Differentialgleichung 
-ter Ordnung
 |
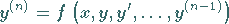(9.22a) |
kann durch Einführung der neuen Variablen
 |
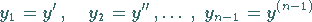(9.22b) |
auf ein System von
Differentialgleichungen 1. Ordnung
 |
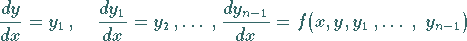(9.22c) |
zurückgeführt werden.
Existenz eines Lösungssystems:
Das im Vergleich zu (9.22c) allgemeinere System von
Differentialgleichungen
 |
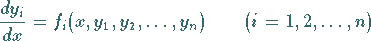(9.23a) |
besitzt ein eindeutig bestimmtes Lösungssystem
 |
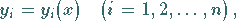(9.23b) |
das in einem Intervall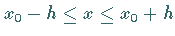 
definiert und stetig ist und für
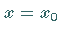die vorgegebenen Anfangswerte 
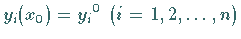annimmt, wenn die Funktionen 
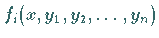bezüglich aller Variablen
stetig sind und die folgende LIPSCHITZ-Bedingung erfüllen.
Die Funktionen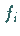 
müssen für die Werte 
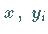und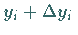 
,
die
in einem gewissen Intervall in der Umgebung der gegebenen Anfangswerte liegen, den
Ungleichungen
mit einer gemeinsamen Konstanten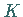 
genügen (s. auch
LIPSCHITZ-Bedingung für Differentialgleichungen 1. Ordnung).
Daraus folgt, vorausgesetzt die Funktion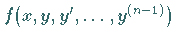 
ist stetig und
erfüllt die LIPSCHITZ-Bedingung (9.24), daß auch die
Gleichung
|
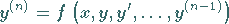(9.25) |
eine eindeutige Lösung besitzt, die die Anfangsbedingungen
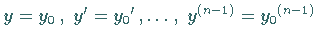für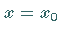
erfüllt und zusammen mit ihren Ableitungen bis einschließlich der 
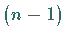-ten
Ordnung stetig ist.
