Existenz einer Lösung, Lipschitz-Bedingung
1. Nach dem Existenzsatz von CAUCHY existiert für die
Differentialgleichung
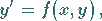 |
(9.2) |
wenigstens eine Lösung, die an der Stelle 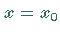 den Wert
den Wert 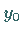 annimmt und in einem
gewissen Intervall um
annimmt und in einem
gewissen Intervall um 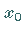 definiert und stetig ist, wenn die Funktion
definiert und stetig ist, wenn die Funktion 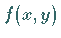 in einer
Umgebung
in einer
Umgebung 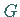 des Punktes
des Punktes 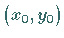 ,
die durch
,
die durch 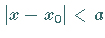 und
und 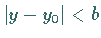 festgelegt ist, stetig ist.
festgelegt ist, stetig ist.
2. Lipschitz-Bedingung bezüglich 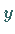 nennt man
die Forderung
nennt man
die Forderung
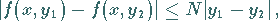 |
(9.3) |
für alle 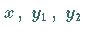 aus
aus 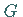 ,
wobei
,
wobei 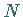 nicht von
nicht von 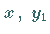 und
und
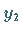 abhängen darf.
Ist sie erfüllt, dann ist die Lösung von (9.2) eindeutig und eine stetige
Funktion von
abhängen darf.
Ist sie erfüllt, dann ist die Lösung von (9.2) eindeutig und eine stetige
Funktion von 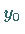 .
Die Erfüllung der LIPSCHITZ-Bedingung ist stets dann gegeben, wenn
.
Die Erfüllung der LIPSCHITZ-Bedingung ist stets dann gegeben, wenn 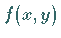 in
dem betrachteten Gebiet eine beschränkte partielle Ableitung
in
dem betrachteten Gebiet eine beschränkte partielle Ableitung 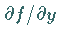 besitzt.
Im Abschnitt Singuläre Integrale und singuläre Punkte sind Fälle
angeführt, in denen die Voraussetzungen des CAUCHYschen Existenzsatzes nicht
erfüllt sind.
besitzt.
Im Abschnitt Singuläre Integrale und singuläre Punkte sind Fälle
angeführt, in denen die Voraussetzungen des CAUCHYschen Existenzsatzes nicht
erfüllt sind.
![]() aus
aus ![]() ,
wobei
,
wobei ![]() nicht von
nicht von ![]() und
und
![]() abhängen darf.
Ist sie erfüllt, dann ist die Lösung von (9.2) eindeutig und eine stetige
Funktion von
abhängen darf.
Ist sie erfüllt, dann ist die Lösung von (9.2) eindeutig und eine stetige
Funktion von ![]() .
Die Erfüllung der LIPSCHITZ-Bedingung ist stets dann gegeben, wenn
.
Die Erfüllung der LIPSCHITZ-Bedingung ist stets dann gegeben, wenn ![]() in
dem betrachteten Gebiet eine beschränkte partielle Ableitung
in
dem betrachteten Gebiet eine beschränkte partielle Ableitung ![]() besitzt.
Im Abschnitt Singuläre Integrale und singuläre Punkte sind Fälle
angeführt, in denen die Voraussetzungen des CAUCHYschen Existenzsatzes nicht
erfüllt sind.
besitzt.
Im Abschnitt Singuläre Integrale und singuläre Punkte sind Fälle
angeführt, in denen die Voraussetzungen des CAUCHYschen Existenzsatzes nicht
erfüllt sind.