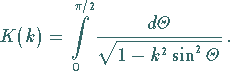Gleichung und Lösungen
Die SG-Gleichung für die Evolutionsfunktion 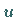 lautet
lautet
 |
(9.141) |
Sie besitzt die folgenden Solitonlösungen:
Kink-Soliton:
 |
(9.142) |
wobei 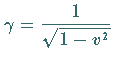 und
und 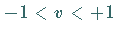 gilt.
gilt.
In der Abbildung ist das Kink-Soliton (9.142) der Gleichung (9.141)
für 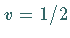 dargestellt.
dargestellt.
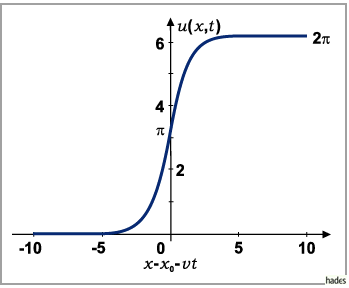
Das Kink-Soliton ist durch die zwei dimensionslosen Parameter 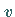 und
und 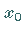 bestimmt,
die Geschwindigkeit ist unabhängig von der Amplitude, die Zeit- und die Ortsableitung
sind gewöhnliche lokalisierte Solitonen:
bestimmt,
die Geschwindigkeit ist unabhängig von der Amplitude, die Zeit- und die Ortsableitung
sind gewöhnliche lokalisierte Solitonen:
 |
(9.143) |
Antikink-Soliton:
 |
(9.144) |
Kink-Antikink-Soliton: Mit  entsteht aus (9.142)
bzw. (9.144) ein statisches Kink-Antikink-Soliton:
entsteht aus (9.142)
bzw. (9.144) ein statisches Kink-Antikink-Soliton:
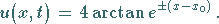 |
(9.145) |
Weitere Lösungen von (9.141) sind:
Kink-Kink-Kollision:
 |
(9.146) |
Kink-Antikink-Kollision:
 |
(9.147) |
Doppel- oder Breather-Soliton, auch Kink-Antikink-Dublett:
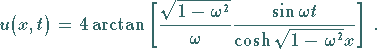 |
(9.148) |
Diese Gleichung (9.148) stellt eine stationäre Welle dar, deren Einhüllende
mit der Frequenz 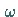 moduliert ist.
moduliert ist.
Örtlich periodisches Kink-Gitter:
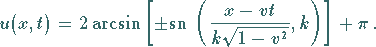 |
(9.149a) |
Zwischen Wellenlänge 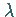 und Gitterkonstante
und Gitterkonstante 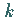 besteht die Beziehung
besteht die Beziehung
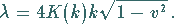 |
(9.149b) |
Für 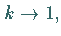 und damit
und damit 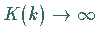 ,
also
,
also
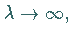 ergibt sich
ergibt sich
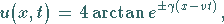 |
(9.149c) |
d.h. wieder das Kink-Soliton (9.142) und das Antikink-Soliton
(9.144) mit 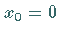 .
.
Hinweis: Mit sn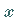 ist eine JACOBIsche elliptische Funktion
mit dem Modul
ist eine JACOBIsche elliptische Funktion
mit dem Modul 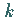 und der Periode
und der Periode 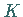 bezeichnet:
bezeichnet:
 |
(9.150a) |
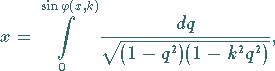 |
(9.150b) |
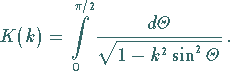 |
(9.150c) |
Die Gleichung (9.150b) geht aus der inversen Funktion
(14.102b) zum elliptischen Integral 1. Gattung
durch die Substitution 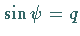 hervor.
hervor.
Die Reihenentwicklung des vollständigen elliptischen Integrals
ist als Gleichung (8.104) angegeben.
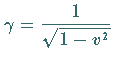 und
und ![]() und Gitterkonstante
und Gitterkonstante ![]() besteht die Beziehung
besteht die Beziehung
![]() und damit
und damit ![]() ,
also
,
also
![]() ergibt sich
ergibt sich
![]() .
.
![]() ist eine JACOBIsche elliptische Funktion
mit dem Modul
ist eine JACOBIsche elliptische Funktion
mit dem Modul ![]() und der Periode
und der Periode ![]() bezeichnet:
bezeichnet: