Zurückblättern Weiterblättern Übergeordnetes Thema Sachgebiet Hauptinhaltsverzeichnis Stichwortverzeichnis Hilfeseiten        


Tangente und Normale


Tangente im Punkt P Tangente im Punkt wird die Sekante in ihrer Grenzlage für genannt, Normale eine Gerade, die im Punkt senkrecht auf der Tangente steht.



Gleichungen der Tangente und der Normalen Die Gleichungen der Tangente und der Normalen sind in der folgenden Tabelle für die drei Fälle der impliziten (3.447), expliziten (3.448) und Parameterform (3.449) angegeben. Dabei sind die Koordinaten des Punktes und die Koordinaten der Tangenten- und Normalenpunkte. Die Werte der Ableitungen sind für den Punkt zu berechnen.

Tabelle Tangenten- und Normalengleichungen
Art der
Gleichung		 Gleichung der Tangente
Gleichung der Normale
(3.447)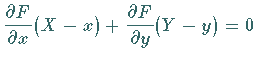
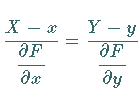(3.448)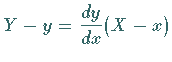
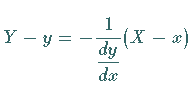(3.449)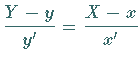

Beispiel A

Kreis mit und Punkt :
a) Tangentengleichung: oder unter Berücksichtigung der Kreisgleichung: , d.h. .
b) Normalengleichung: oder im Punkt .

Beispiel B

Sinuslinie im Punkt :
a) Tangentengleichung: oder im Punkt
b) Normalengleichung: oder im Punkt

Beispiel C

Kurve mit im Punkt
a) Tangentengleichung: oder im Punkt
b) Normalengleichung: oder im Punkt


Positive Richtung von Kurventangente und Kurvennormale Wenn die Kurve in der expliziten (3.448), Parameter- (3.449) oder Polarkoordinatenform (3.450) gegeben ist, dann sind die positiven Richtungen auf der Tangente und der Normalen festgelegt. Die positive Richtung auf der Tangente stimmt mit der positiven Richtung der Kurve im Berührungspunkt überein, während sich die positive Richtung auf der Normalen aus der positiven Richtung der Tangente durch deren Drehung um den Punkt um im entgegengesetzten Drehsinn des Uhrzeigers ergibt.



Die Tangente und die Normale werden durch den Punkt jeweils in eine positive und eine negative Halbgerade geteilt.
Steigung der Tangente Die Steigung der Tangente wird bestimmt
a) durch den Tangentenneigungswinkel zwischen den positiven Richtungen der Abszissenachse und der Tangente oder,
b) wenn die Kurve in Polarkoordinaten gegeben ist, durch den Winkel zwischen der Richtung des Radiusvektors und der positiven Richtung der Tangente.



Für die Winkel und gelten die folgenden Formeln, wobei das Bogenelement gemäß (3.451) bis (3.453) berechnet wird:
(3.454a)
(3.454b)

Beispiel A

 

Beispiel B


Beispiel C

 


Abschnitte der Tangente und Normale, Subtangente und Subnormale Man erhält in Anlehnung an die Abbildung die folgenden Formeln:




a) In kartesischen Koordinaten für eine Definition gemäß der expliziten Definition (3.448):
(3.455a)

(3.455b)

(3.455c)

(3.455d)


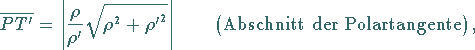b) In Polarkoordinaten für eine Definition gemäß der Polarkoordinatenform (3.450):
(3.456a)

(3.456b)

(3.456c)

(3.456d)


Beispiel A



Beispiel B




Winkel zwischen zwei Kurven Unter dem Winkel zwischen zwei Kurven und die sich im Punkt schneiden, wird der Winkel zwischen den Tangenten an diese Kurven im Punkt verstanden.



Die Berechnung des Winkels ist damit auf die Berechnung des Winkels zwischen zwei Geraden mit den Richtungskoeffizienten
(3.457a)

(3.457b)

zurückgeführt, wobei die Gleichung von und die Gleichung von ist und die Ableitungen für den Punkt zu berechnen sind.
Beispiel

Es ist der Winkel zwischen den Parabeln und im Punkt zu bestimmen:
.