|
Integration der Funktion 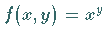 über dem Rechteck
über dem Rechteck
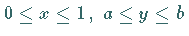 .
Die Funktion .
Die Funktion 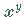 ist bei
ist bei 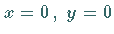 unstetig, für
unstetig, für 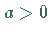 ist sie stetig.
Daher kann die Integrationsreihenfolge gemäß
ist sie stetig.
Daher kann die Integrationsreihenfolge gemäß
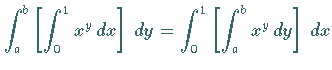 vertauscht werden.
Links erhält man
vertauscht werden.
Links erhält man 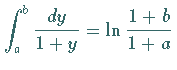 ,
rechts ,
rechts
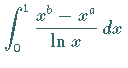 .
Das unbestimmte Integral kann nicht durch elementare Funktionen ausgedrückt werden.
Das bestimmte Integral ist allerdings bekannt, so daß sich ergibt .
Das unbestimmte Integral kann nicht durch elementare Funktionen ausgedrückt werden.
Das bestimmte Integral ist allerdings bekannt, so daß sich ergibt
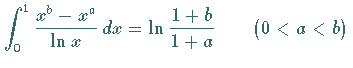 . .
|