Differentiation unter dem Integralzeichen

Differentiation unter dem Integralzeichen

1. Satz: Wenn die Funktion (8.90) im Intervall

definiert ist und die Funktion

im Rechteck

stetig ist und eine partielle Ableitung nach

besitzt, dann gilt bei beliebigem

im Intervall

(8.92)

Man spricht vom Differenzieren unter dem Integralzeichen .

Beispiel

Für beliebig:
.
Probe: . Für ist die Stetigkeitsbedingung nicht erfüllt, so daß hier keine Ableitung existiert.

2. Verallgemeinerung auf parameterabhängige Integrationsgrenzen: Die Formel (8.92) kann verallgemeinert werden, wenn die Funktionen und unter den gleichen Bedingungen, die für (8.92) gefordert werden, im Intervall definiert, stetig und differenzierbar sind und wenn die Kurven das Rechteck nicht verlassen:

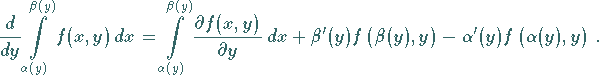(8.93)

Beispiel
	Für beliebig: . Probe: . Für ist die Stetigkeitsbedingung nicht erfüllt, so daß hier keine Ableitung existiert.