Zusammenhang zwischen uneigentlichen Integralen und unendlichen Reihen
Wenn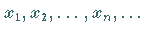 
eine beliebige, unbegrenzt wachsende unendliche Folge
ist, d.h. wenn gilt
 |
(8.84a) |
und wenn die Funktion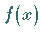 
positiv für 
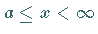ist, dann kann
die Frage nach der Konvergenz des Integrals (8.77) auf die
Frage nach der Konvergenz der Reihe
 |
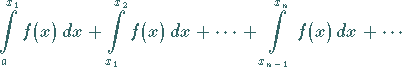(8.84b) |
zurückgeführt werden.
Wenn die Reihe (8.84b) konvergiert, dann konvergiert auch das Integral
(8.77) und es ist dann gleich der Summe der Reihe (8.84b).
Divergiert die Reihe (8.84b), dann divergiert auch das Integral
(8.77).
Somit können die Konvergenzkriterien für Reihen auch zur Konvergenzuntersuchung von
Integralen eingesetzt werden.
Beim Integralkriterium für Reihen wird umgekehrt die
Konvergenzuntersuchung der Reihen auf die Untersuchung der Konvergenz eines uneigentlichen
Integrals zurückgeführt.
