Konvergenz und Hauptwert des uneigentlichen Integrals
a) Wenn das Integrationsgebiet die abgeschlossene Halbachse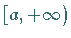 
ist,
und wenn der Integrand dort definiert ist, dann gilt definitionsgemäß
 |
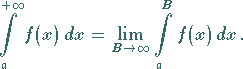(8.77) |
Im Falle der Existenz des Grenzwertes spricht man von einem konvergenten
uneigentlichen Integral .
Im Falle der Nichtexistenz des Grenzwertes wird (8.77) als divergentes Integral
bezeichnet.
b) Wenn das Definitionsgebiet einer Funktion die abgeschlossene Halbachse
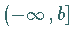oder die gesamte Zahlengerade 
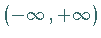ist, dann definiert man analog
 |
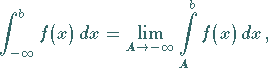(8.78a) |
 |
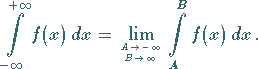(8.78b) |
c) Beim Grenzübergang (8.78b) streben die Zahlen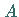 
und 
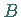unabhängig voneinander gegen unendlich.
Wenn der Grenzwert (8.78b) dabei nicht existiert, dafür jedoch der Grenzwert
 |
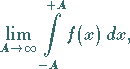(8.78c) |
dann heißt dieser Grenzwert (8.78c)
Hauptwert des uneigentlichen Integrals .
