|
|
|
|
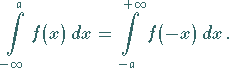 |
(8.79) |
Das Integral vom Typ (8.78b) wird in eine Summe aus zwei Integralen vom Typ (8.77) und vom Typ (8.78a) zerlegt:
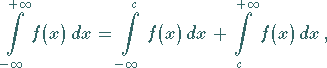 |
(8.80) |
wobei ![]() eine beliebige Zahl ist.
eine beliebige Zahl ist.
1. Kriterium: Wenn das Integral
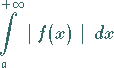 |
(8.81) |
existiert, dann existiert auch das Integral (8.77).
Das Integral (8.77) heißt in diesem Falle
absolut konvergent und die Funktion ![]() absolut integrierbar
auf der Halbachse
absolut integrierbar
auf der Halbachse ![]() .
.
2. Kriterium: Gilt für die Funktionen ![]() und
und ![]()
| (8.82a) |
| (8.83a) |
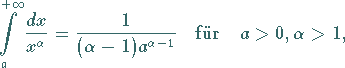 |
(8.83b) |
| (8.83c) |
gilt, dann konvergiert das Integral (8.77).
Wenn allerdings ![]() positiv ist und eine Zahl
positiv ist und eine Zahl ![]() existiert, so daß
existiert, so daß
| (8.83d) |
von einer gewissen Stelle an gilt, dann divergiert das Integral
(8.77).
| Beispiel | |
|
| |
|
|
|