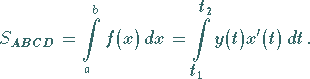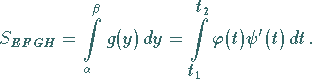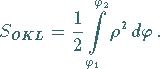Flächeninhalte ebener Flächen
1. Flächeninhalt eines zwischen den Punkten  und
und 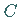 krummlinig begrenzten
Trapezes:
Der Flächeninhalt eines oben zwischen den Punkten
krummlinig begrenzten
Trapezes:
Der Flächeninhalt eines oben zwischen den Punkten 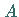 und
und 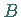 krummlinig begrenzten
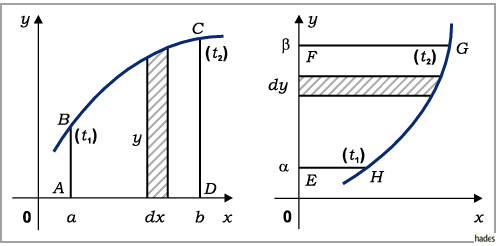
Trapezes (s. linke Abbildung) bei explizit (
krummlinig begrenzten
Trapezes (s. linke Abbildung) bei explizit (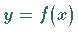 und
und 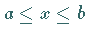 )
bzw. in
Parameterform (
)
bzw. in
Parameterform (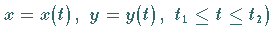 gegebener
Kurvengleichung:
gegebener
Kurvengleichung:
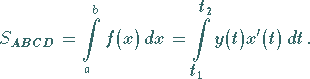 |
(8.59a) |
2. Flächeninhalt eines seitlich zwischen den Punkten 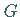 und
und 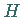 krummlinig
begrenzten Trapezes:
Der Flächeninhalt eines seitlich zwischen den Punkten
krummlinig
begrenzten Trapezes:
Der Flächeninhalt eines seitlich zwischen den Punkten 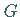 und
und 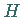 krummlinig begrenzten
Trapezes (s. rechte Abbildung) bei explizit (
krummlinig begrenzten
Trapezes (s. rechte Abbildung) bei explizit (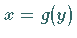 und
und 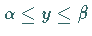 )
bzw. in Parameterform (
)
bzw. in Parameterform (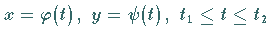 )
gegebener Kurvengleichung:
)
gegebener Kurvengleichung:
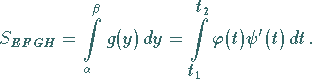 |
(8.59b) |
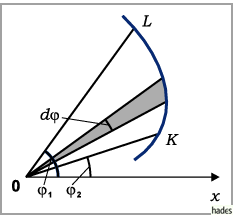
3. Flächeninhalt eines Kurvensektors:
Der Flächeninhalt eines Kurvensektors (s. Abbildung), begrenzt durch ein Kurvenstück
zwischen den Punkten 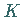 und
und 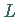 ,
das mit einer in Polarkoordinaten gegebenen
Kurvengleichung (
,
das mit einer in Polarkoordinaten gegebenen
Kurvengleichung (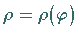 ,
,
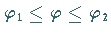 )
beschrieben wird:
)
beschrieben wird:
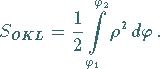 |
(8.59c) |
Flächeninhalte von komplizierteren Figuren werden mit Hilfe des
Kurvenintegrals oder mit Hilfe des
Doppelintegrals berechnet.
Allgemeine Formeln zur Berechnung von Flächen mit Hilfe von Doppelintegralen sind in
der Tabelle Anwendung von Doppelintegralen angegeben.