|
|
|
|
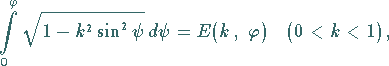 |
(8.23b) |
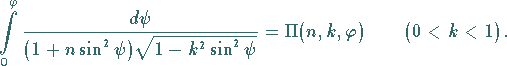 |
(8.23c) |
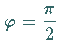 heißen die ersten beiden Integrale
vollständige elliptische Integrale , und man kennzeichnet sie durch
heißen die ersten beiden Integrale
vollständige elliptische Integrale , und man kennzeichnet sie durch
| Beispiel | |
|
Die Berechnung des Umfanges der Ellipse führt auf ein
vollständiges elliptisches Integral 2. Gattung als Funktion der numerischen
Exzentrizität | |
|
|
|