|
|
|
|
 |
(8.20b) |
Sie lassen sich in der Regel nicht durch elementare Funktionen ausdrücken; wenn dies
trotzdem gelingt, nennt man sie pseudoelliptisch.
Ausgangspunkt für die Bezeichnung war das erstmalige Auftreten eines derartigen
Integrals bei der Berechnung des Umfanges der Ellipse.
Die Umkehrung der elliptischen Integrale sind die
elliptischen Funktionen.
Integrale der Art (8.20a,b), die nicht elementar integrierbar
sind, können durch eine Reihe von Umformungen auf elementare Funktionen und auf
Integrale der folgenden drei Typen zurückgeführt werden (s. Lit. 21.1,
21.2, 21.6):
in (8.21c) sind Fallunterscheidungen notwendig
(s. Lit. 14.1).
Mit Hilfe der Substitution
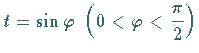können die Integrale
(8.21a,b,c) auf die LEGENDREsche Form
gebracht werden:
|
|
