Berechnung des Dreifachintegrals in beliebigen krummlinigen Koordinaten
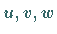
Die beliebigen krummlinigen Koordinaten sind durch die Beziehungen
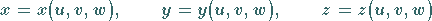 |
(8.146) |
definiert.
Das Integrationsgebiet wird durch die Koordinatenflächen
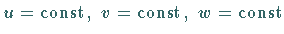 in infinitesimale
Volumenelemente in beliebigen Koordinaten eingeteilt:
in infinitesimale
Volumenelemente in beliebigen Koordinaten eingeteilt:
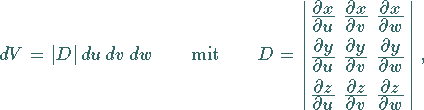 |
(8.147a) |
wobei 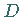 die Funktionaldeterminante ist.
Nach Ausdrücken des Integranden in den Koordinaten
die Funktionaldeterminante ist.
Nach Ausdrücken des Integranden in den Koordinaten 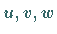 lautet das Integral:
lautet das Integral:
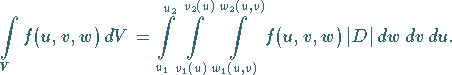 |
(8.147b) |
Die Formeln (8.144b) und (8.145b) sind Spezialfälle von
(8.147b).
Für Zylinderkoordinaten ist 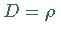 ,
für Kugelkoordinaten ist
,
für Kugelkoordinaten ist
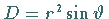 .
Mit Vorteil werden immer solche krummlinigen Koordinaten verwendet, die eine möglichst
einfache Berechnung der Integrationsgrenzen des Integrals (8.147b)
gestatten.
.
Mit Vorteil werden immer solche krummlinigen Koordinaten verwendet, die eine möglichst
einfache Berechnung der Integrationsgrenzen des Integrals (8.147b)
gestatten.
![]() in infinitesimale
Volumenelemente in beliebigen Koordinaten eingeteilt:
in infinitesimale
Volumenelemente in beliebigen Koordinaten eingeteilt:
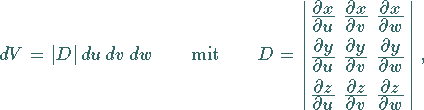
![]() die Funktionaldeterminante ist.
Nach Ausdrücken des Integranden in den Koordinaten
die Funktionaldeterminante ist.
Nach Ausdrücken des Integranden in den Koordinaten ![]() lautet das Integral:
lautet das Integral: