Umlaufintegral
1. Begriff des Umlaufintegrals:
Ein Umlaufintegral ist ein Kurvenintegral über einen geschlossenen
Integrationsweg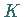 
,
d.h., der Anfangspunkt 
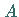ist mit dem Endpunkt 
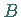identisch.
Man schreibt dafür:
 |
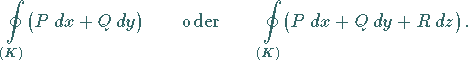(8.122) |
Im allgemeinen ist das Umlaufintegral verschieden von Null.
Das gilt jedoch nicht, wenn die Integrabilitätsbedingung
erfüllt ist oder wenn die Integration in einem konservativen Feld
durchzuführen ist. Siehe auch Verschwinden des Umlaufintegrals.
2. Berechnung des Flächeninhaltes einer ebenen Figur:
Die Berechnung des Flächeninhaltes einer ebenen Figur ist ein typisches Beispiel für
die Anwendung des Umlaufintegrals in der Form
 |
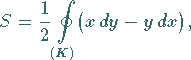(8.123) |
wobei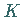 
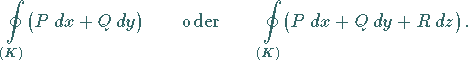
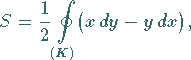
die Randkurve der ebenen Figur ist.
Der Integrationsweg wird positiv gerechnet, wenn er entgegengesetzt zum Drehsinn des
Uhrzeigers verläuft.
