Definition des konservativen Feldes
Von einem konservativen Feld oder einem Potentialfeld spricht man,
wenn der Wert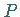 
des Kurvenintegrals (13.96a) in einem Vektorfeld
nur von der Lage der Punkte 
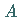und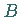 
abhängt und nicht vom konkreten Integrationsweg
zwischen diesen beiden Punkten.
Der Zahlenwert des Umlaufintegrals in einem konservativen Feld ist stets gleich Null:
 |
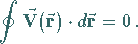(13.103) |
Ein konservatives Feld zeichnet sich immer durch Wirbelfreiheit aus:
 |
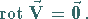(13.104) |
Umgekehrt ist diese Gleichung die notwendige und hinreichende Bedingung dafür, daß
das Feld konservativ ist.
Dazu muß weiterhin vorausgesetzt werden, daß die partiellen Ableitungen der
Feldfunktion nach den enthaltenen Koordinaten stetig sind und der Definitionsbereich von
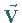einfach zusammenhängend ist.
Für ein dreidimensionales Feld hat dieser,
Integrabilitätsbedingung genannte Zusammenhang in kartesischen
Koordinaten die Form
 |
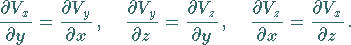(13.105) |
