Zweidimensionaler Fall
1. Definition: Wenn das Kurvenintegral
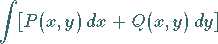 |
(8.124) |
mit den stetigen Funktionen 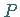 und
und 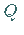 ,
die in einem einfach zusammenhängenden Gebiet
definiert sind, nur vom Anfangspunkt
,
die in einem einfach zusammenhängenden Gebiet
definiert sind, nur vom Anfangspunkt 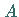 und vom Endpunkt
und vom Endpunkt 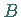 abhängen soll, nicht aber
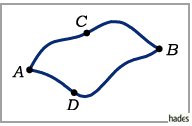
vom Integrationsweg, der beide Punkte verbindet (s. Abbildung), d.h. für beliebige
abhängen soll, nicht aber
vom Integrationsweg, der beide Punkte verbindet (s. Abbildung), d.h. für beliebige 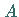 und
und 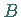 und beliebige Integrationswege
und beliebige Integrationswege 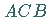 bzw.
bzw. 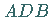 die Gleichung
die Gleichung
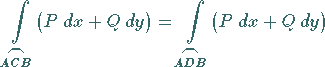 |
(8.125) |
gelten soll, dann ist notwendig und hinreichend, daß eine Funktion 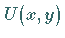 von zwei
Veränderlichen existiert, deren vollständiges Differential der Integrand des
Kurvenintegrals ist:
von zwei
Veränderlichen existiert, deren vollständiges Differential der Integrand des
Kurvenintegrals ist:
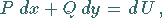 |
(8.126a) |
d.h., es gilt
 |
(8.126b) |
Die Funktion 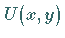 ist dann eine Stammfunktion des vollständigen Differentials
(8.126a).
ist dann eine Stammfunktion des vollständigen Differentials
(8.126a).
In der Physik wird die Stammfunktion 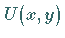 als
Potential in einem Vektorfeld gedeutet.
als
Potential in einem Vektorfeld gedeutet.
2. Existenz der Stammfunktion:Notwendiges und hinreichendes Kriterium für die Existenz der Stammfunktion , die
Integrabilitätsbedingung für den Ausdruck
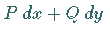 ,
ist die Gleichheit der partiellen Ableitungen
,
ist die Gleichheit der partiellen Ableitungen
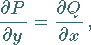 |
(8.127) |
von denen gefordert werden muß, daß sie stetig sind.
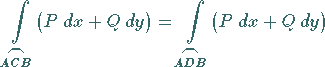
![]() ist dann eine Stammfunktion des vollständigen Differentials
(8.126a).
ist dann eine Stammfunktion des vollständigen Differentials
(8.126a).