Stellt man eine Funktion 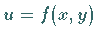 als Fläche in einem kartesischen Koordinatensystem
dar und legt man durch den Flächenpunkt
als Fläche in einem kartesischen Koordinatensystem
dar und legt man durch den Flächenpunkt 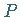 eine Ebene parallel zur
eine Ebene parallel zur 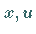 -Ebene, dann
gilt
-Ebene, dann
gilt
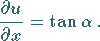 |
(6.36a) |
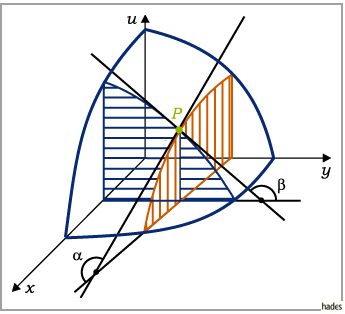
Dabei ist 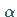 der Winkel zwischen der positiven
der Winkel zwischen der positiven 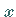 -Achse und der Tangente an die
Schnittkurve der Fläche in dem betreffenden Punkt mit einer Ebene, die parallel zur
-Achse und der Tangente an die
Schnittkurve der Fläche in dem betreffenden Punkt mit einer Ebene, die parallel zur
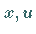 -Ebene verläuft.
Die Messung von
-Ebene verläuft.
Die Messung von 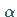 erfolgt, ausgehend von der
erfolgt, ausgehend von der 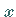 -Achse zur Tangente an die
Schnittkurve, im entgegengesetzten Drehsinn des Uhrzeigers.
Dabei ist der Blick von der positiven
-Achse zur Tangente an die
Schnittkurve, im entgegengesetzten Drehsinn des Uhrzeigers.
Dabei ist der Blick von der positiven 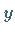 -Achse gegen die Schnittebene gerichtet.
In Analogie zu
-Achse gegen die Schnittebene gerichtet.
In Analogie zu 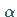 ist
ist 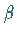 gemäß
gemäß
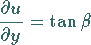 |
(6.36b) |
definiert.
Bezüglich der Ableitung nach einer gegebenen Richtung
s. Richtungsableitung bzw. nach einem Volumen
s. Volumenableitung.