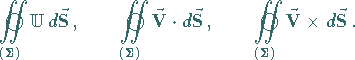Volumenableitung oder räumliche Ableitung
Als Volumenableitung eines Skalarfeldes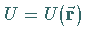 
oder eines Vektorfeldes
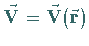in einem Punkt 
werden drei
Größen bezeichnet, die folgendermaßen gewonnen werden:
1. Einhüllung eines Punktes
des Skalarfeldes 
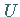oder des
Vektorfeldes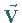 
durch eine geschlossene Fläche 
.
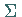Diese Fläche lasse sich vektoriell durch die Parameterdarstellung
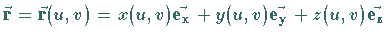beschreiben, so daß das zugehörige vektorielle Flächenelement
 |
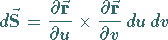(13.31a) |
lautet.
2. Integration über die geschlossene Fläche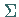 
.
Dabei werden die folgenden drei Typen von Integralen betrachtet:
 |
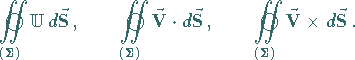(13.31b) |
3.
Bestimmung der Grenzwerte
 |
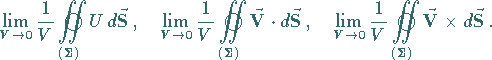(13.31c) |
Dabei wird mit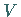 
das Volumen des Raumteiles bezeichnet, der den Punkt
im
Innern enthält und dessen Oberfläche die geschlossene Fläche
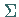ist.
Die Grenzwerte (13.31c) werden als Volumenableitungen bezeichnet und führen in
der angegebenen Reihenfolge auf die Begriffe Gradient eines Skalarfeldes sowie
Divergenz und Rotation eines Vektorfeldes.
