|
Es wird eine dreidimensionale Darstellung der symmetrischen Gruppe 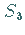 betrachtet.
Von drei Teilchen mit den Koordinaten
betrachtet.
Von drei Teilchen mit den Koordinaten 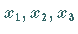 besetzen in einem Schalenmodell
der Atom- oder Kernphysik zwei Teilchen den Zustand
besetzen in einem Schalenmodell
der Atom- oder Kernphysik zwei Teilchen den Zustand 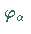 ,
und ein
Teilchen befindet sich im Zustand ,
und ein
Teilchen befindet sich im Zustand 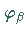 (Konfiguration
(Konfiguration 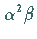 ).
Die möglichen Besetzungen ).
Die möglichen Besetzungen
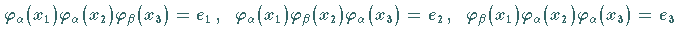 bilden eine Basis
bilden eine Basis 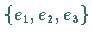 in einem dreidimensionalen Vektorraum
in einem dreidimensionalen Vektorraum 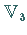 zur Darstellung der symmetrischen Gruppe
zur Darstellung der symmetrischen Gruppe 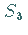 .
Die Matrixelemente der Darstellungsmatrizen können entsprechend (5.108)
durch Anwendung der Gruppenelemente (5.92) auf die Koordinatenindizes in
den Basiselementen .
Die Matrixelemente der Darstellungsmatrizen können entsprechend (5.108)
durch Anwendung der Gruppenelemente (5.92) auf die Koordinatenindizes in
den Basiselementen 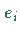 gwonnen werden.
So gilt z.B.:
gwonnen werden.
So gilt z.B.:
Man findet insgesamt:
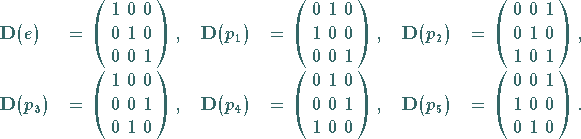 |
(5.117) |
Für die Charaktere ergibt sich:
|