Äquivalente Darstellungen
Zwei Darstellungen 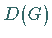 und
und 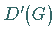 nennt man äquivalent , wenn
für jedes Gruppenelement
nennt man äquivalent , wenn
für jedes Gruppenelement 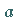 die Darstellungsmatrizen durch die gleiche
Ähnlichkeitstransformation mit der nichtsingulären Matrix
die Darstellungsmatrizen durch die gleiche
Ähnlichkeitstransformation mit der nichtsingulären Matrix 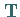 auseinander
hervorgehen:
auseinander
hervorgehen:
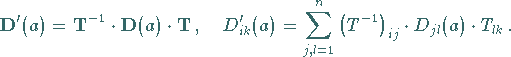 |
(5.113) |
Im entgegengesetzten Falle spricht man von einer inäquivalenten Darstellung .
Der Übergang von 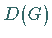 nach
nach 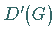 entspricht einer Basistransformation
entspricht einer Basistransformation
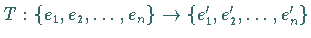 im Darstellungsraum
im Darstellungsraum
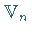 :
:
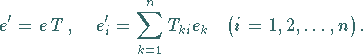 |
(5.114) |
Jede Darstellung einer endlichen Gruppe ist einer unitären Darstellung
äquivalent.