Eine Darstellung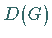 
der Gruppe 
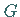ist eine Abbildung
(Homomorphismus) von
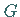auf die Gruppe nichtsingulärer linearer Transformationen
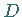in einem 
-dimensionalen (reellen oder komplexen) Vektorraum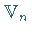 
:
 |
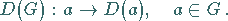(5.105) |
Der Vektorraum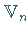 
heißt Darstellungsraum ;
ist die Dimension der
Darstellung (s. auch Vektorräume).
Nach Einführung einer Basis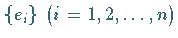 
in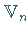
kann
jeder Vektor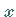 
als Linearkombination der Basisvektoren geschrieben werden:
 |
(5.106) |
Die Wirkung der linearen Transformation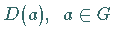 
auf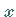
läßt sich durch eine quadratische Matrix
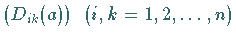definieren, die die Koordinaten des transformierten Vektors 
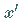in der Basis
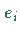liefert:
 |
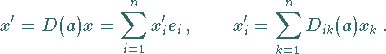(5.107) |
Diese Transformation kann auch als Basistransformation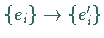 
aufgefaßt werden:
 |
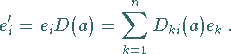(5.108) |
Damit wird jedem Gruppenelement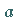 
eine Darstellungsmatrix
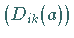zugeordnet:
 |
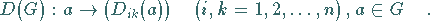(5.109) |
Die Darstellungsmatrix hängt von der Wahl der Basis ab.
