Kongruenzrelationen, Faktoralgebren
Um Faktorstrukturen, wie im Falle der Gruppen und Ringe, für universelle Algebren
konstruieren zu können, wird der Begriff der Kongruenzrelation benötigt.
Eine Kongruenzrelation ist eine mit der Struktur verträgliche Äquivalenzrelation:
Es sei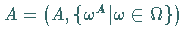 
eine 
-Algebra und 
eine
Äquivalenzrelation in 
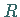heißt Kongruenzrelation in 
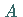falls für alle
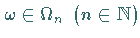und alle 
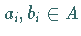mit
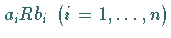gilt:
 |
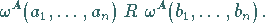(5.291) |
Die Menge der Äquivalenzklassen (Faktormenge) bezüglich einer Kongruenzrelation
bildet bezüglich repräsentantenweisem Rechnen wieder eine 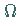-Algebra:
Es sei
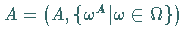eine 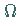-Algebra und
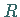eine
Kongruenzrelation in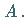 
Die Faktormenge 
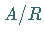(s. Äquivalenz- und Ordnungsrelationen)
wird bezüglich folgender Operationen 
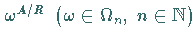mit
 |
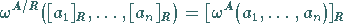(5.292) |
zu einer 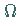-Algebra 
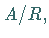der Faktoralgebra von 
nach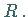 
Die Kongruenzrelationen von Gruppen bzw. Ringen lassen sich durch spezielle
Teilstrukturen - Normalteiler bzw. Ideale -
beschreiben.
Im allgemeinen, z.B. bei Halbgruppen, ist eine solche Beschreibung der Kongruenzrelationen
nicht möglich.
