Unterringe, Ideale
1. Unterring: Es sei 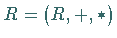 ein Ring und
ein Ring und 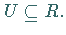 Ist
Ist 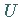 bezüglich
bezüglich 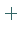 und
und  wieder ein Ring, so heißt
wieder ein Ring, so heißt 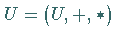 ein
Unterring von
ein
Unterring von 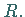
Eine nichtleere Teilmenge 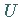 eines Ringes
eines Ringes 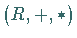 bildet genau dann einen Unterring
von
bildet genau dann einen Unterring
von 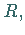 wenn für alle
wenn für alle 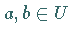 auch
auch 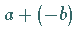 und
und 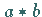 in
in 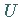 liegen
( Unterringkriterium ).
liegen
( Unterringkriterium ).
2. Ideal: Ein Unterring 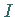 heißt Ideal , wenn für alle
heißt Ideal , wenn für alle 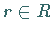 und
und
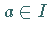 sowohl
sowohl  als auch
als auch  in
in 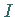 liegen.
Diese speziellen Unterringe sind die Grundlage für die Bildung von
Faktorringen.
liegen.
Diese speziellen Unterringe sind die Grundlage für die Bildung von
Faktorringen.
Die trivialen Unterringe 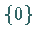 und
und 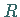 sind auch stets Ideale von
sind auch stets Ideale von 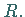 Körper haben nur triviale Ideale.
Körper haben nur triviale Ideale.
3. Hauptideal:
Sämtliche Ideale von 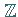 sind Hauptideale , d.h. Ideale, die von einem Ringelement
,,erzeugt`` werden können.
Sie werden in der Form
sind Hauptideale , d.h. Ideale, die von einem Ringelement
,,erzeugt`` werden können.
Sie werden in der Form 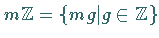 geschrieben und mit
geschrieben und mit 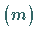 bezeichnet.
bezeichnet.