Definition der Omega-Algebra
Es sei 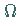 eine Menge von Operationssymbolen, die in paarweise disjunkte Teilmengen
eine Menge von Operationssymbolen, die in paarweise disjunkte Teilmengen
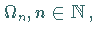 zerfällt.
In
zerfällt.
In 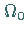 liegen die Konstanten, in
liegen die Konstanten, in 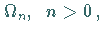 die
die  -stelligen
Operationssymbole.
Die Familie
-stelligen
Operationssymbole.
Die Familie  heißt Typ oder Signatur .
Ist
heißt Typ oder Signatur .
Ist  eine Menge und ist jedem
eine Menge und ist jedem  -stelligen Operationssymbol
-stelligen Operationssymbol 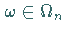 eine
eine
 -stellige Operation
-stellige Operation 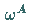 in
in  zugeordnet, so heißt
zugeordnet, so heißt
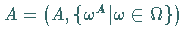 eine
eine 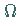 - Algebra oder Algebra
vom Typ (oder der Signatur)
- Algebra oder Algebra
vom Typ (oder der Signatur) 
Ist  endlich,
endlich, 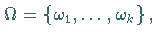 so schreibt man für
so schreibt man für
 auch
auch 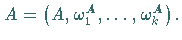
Faßt man einen Ring als  -Algebra auf, so zerfällt
-Algebra auf, so zerfällt
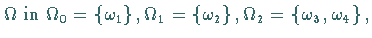 wobei den Operationssymbolen
wobei den Operationssymbolen
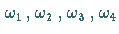 die Konstante 0, Inversenbildung
bezüglich Addition, Addition und Multiplikation zugeordnet sind.
die Konstante 0, Inversenbildung
bezüglich Addition, Addition und Multiplikation zugeordnet sind.
Es seien  und
und 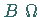 -Algebren.
-Algebren. 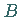 heißt
heißt 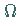 -Unteralgebra von
-Unteralgebra von
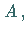 falls
falls 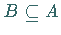 ist und die Operationen
ist und die Operationen 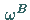 die Einschränkungen
der Operationen
die Einschränkungen
der Operationen 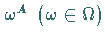 auf die Teilmenge
auf die Teilmenge 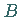 sind.
sind.