Homomorphismen
Wie bei den klassischen algebraischen Strukturen besteht auch hier über den
Homomorphiesatz ein Zusammenhang zwischen den Homomorphismen und den Kongruenzrelationen.
Es seien 
und 
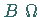-Algebren.
Eine Abbildung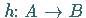 
heißt Homomorphismus , wenn für jedes
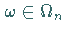und alle 
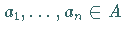gilt:
 |
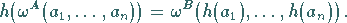(5.293) |
Ist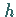 
darüber hinaus bijektiv, so heißt
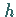Isomorphismus ; die Algebren
und 
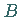heißen dann zueinander isomorph.
Das homomorphe Bild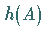 
einer 
-Algebra
erweist sich als
-Unteralgebra von 
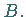Bei einem Homomorphismus
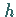entspricht der Zerlegung von
in bildgleiche Elemente
eine Kongruenzrelation, die der Kern von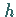
genannt wird:
 |
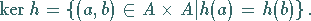(5.294) |
