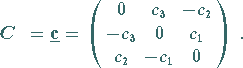Das Tensorprodukt der axialen Vektoren 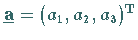 und
und
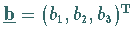 ergibt gemäß (4.73a) einen
Tensor 2. Stufe mit den Komponenten
ergibt gemäß (4.73a) einen
Tensor 2. Stufe mit den Komponenten 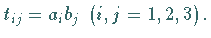 Da sich jeder Tensor 2. Stufe als Summe eines symmetrischen und eines schiefsymmetrischen
Tensors 2. Stufe darstellen läßt, gilt wegen (4.80)
Da sich jeder Tensor 2. Stufe als Summe eines symmetrischen und eines schiefsymmetrischen
Tensors 2. Stufe darstellen läßt, gilt wegen (4.80)
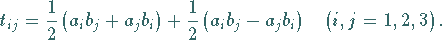 |
(4.101) |
Der schiefsymmetrische Anteil in dieser Gleichung ergibt bis auf den Faktor
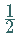 gerade die Komponenten des Vektorprodukts
gerade die Komponenten des Vektorprodukts
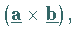 so daß man den axialen Vektor
so daß man den axialen Vektor
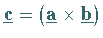 mit den Komponenten
mit den Komponenten
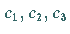 auch als schiefsymmetrischen Tensor 2. Stufe
auch als schiefsymmetrischen Tensor 2. Stufe
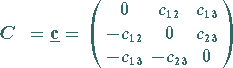 |
(4.102a) |
mit
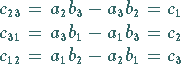 |
(4.102b) |
auffassen kann, dessen Komponenten die Transformationsformel (4.100b) für
Tensoren 2. Stufe erfüllen.
Damit kann man jeden axialen Vektor (Pseudovektor oder Pseudotensor 1. Stufe)
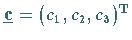 als schiefsymmetrischen Tensor 2. Stufe
als schiefsymmetrischen Tensor 2. Stufe
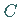 auffassen, wobei gilt
auffassen, wobei gilt
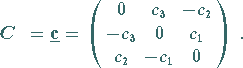 |
(4.103) |
![]() gerade die Komponenten des Vektorprodukts
gerade die Komponenten des Vektorprodukts
![]() so daß man den axialen Vektor
so daß man den axialen Vektor
![]() mit den Komponenten
mit den Komponenten
![]() auch als schiefsymmetrischen Tensor 2. Stufe
auch als schiefsymmetrischen Tensor 2. Stufe
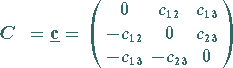
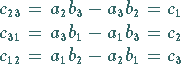
![]() als schiefsymmetrischen Tensor 2. Stufe
als schiefsymmetrischen Tensor 2. Stufe
![]() auffassen, wobei gilt
auffassen, wobei gilt