|
|
|
|
bzw.
mit den Komponenten
bzw. 
seien von der Stufe 
bzw. 
Dann bilden die 
Skalare
der Stufe 
Man schreibt
=
und spricht vom
Tensorprodukt von
und
.
Es gelten Assioziativ- und Distributivgesetz:
 |
(4.73b) |
3. Dyadisches Produkt:
Das Produkt zweier Tensoren 1. Stufe
und
ergibt einen Tensor 2. Stufe mit den Elementen
 |
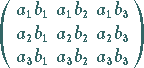(4.74b) |
dar.
Diese wird auch als dyadisches Produkt der beiden Vektoren 
und
bezeichnet.
4. Verjüngung:
Setzt man in einem Tensor der Stufe 
zwei Indizes gleich und summiert
über sie, so erhält man einen Tensor der Stufe 
und spricht von einer
Verjüngung des Tensors.
| Beispiel | |||
|
Der 2stufige Tensor
einen Skalar, also einen Tensor nullter Stufe erhält. Er stellt das Skalarprodukt der Vektoren 
und 
dar.
| |||
|
|
der das Tensorprodukt der beiden Vektoren
und 
darstellt, wird über die Indizes 
und 
verjüngt, so daß man mit
