Epsilontensor
Sind 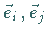 und
und 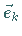 die Einheitsvektoren in Richtung der
Achsen eines rechtwinkligen Koordinatensystems, dann gilt für das
Spatprodukt
die Einheitsvektoren in Richtung der
Achsen eines rechtwinkligen Koordinatensystems, dann gilt für das
Spatprodukt
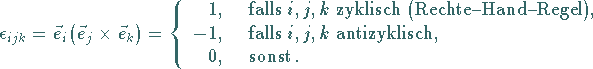 |
(4.79a) |
Das sind insgesamt  Elemente, die als Elemente eines 3stufigen Tensors
aufgefaßt werden können.
Im Falle einer Drehung des Koordinatensystems folgt aus dem Transformationsgesetz
(4.68)
Elemente, die als Elemente eines 3stufigen Tensors
aufgefaßt werden können.
Im Falle einer Drehung des Koordinatensystems folgt aus dem Transformationsgesetz
(4.68)
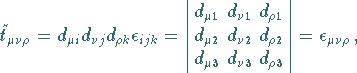 |
(4.79b) |
d.h., die Elemente sind drehungsinvariant .
Paßt man sie so in ein Koordinatensystem ein, daß sie unabhängig von der Wahl
des Ursprungs, also auch translationsinvariant sind, dann bilden die Zahlen
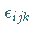 einen invarianten Tensor 3. Stufe, den sogenannten Epsilontensor .
einen invarianten Tensor 3. Stufe, den sogenannten Epsilontensor .
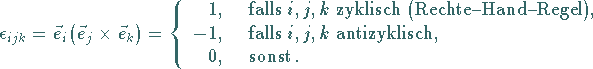
![]() Elemente, die als Elemente eines 3stufigen Tensors
aufgefaßt werden können.
Im Falle einer Drehung des Koordinatensystems folgt aus dem Transformationsgesetz
(4.68)
Elemente, die als Elemente eines 3stufigen Tensors
aufgefaßt werden können.
Im Falle einer Drehung des Koordinatensystems folgt aus dem Transformationsgesetz
(4.68)
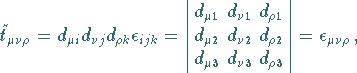
![]() einen invarianten Tensor 3. Stufe, den sogenannten Epsilontensor .
einen invarianten Tensor 3. Stufe, den sogenannten Epsilontensor .