Die praktische Durchführung der Transformation (4.135) erfolgt
über die Hauptachsentransformation (4.129).
Anschaulich bedeutet dieses Vorgehen, daß zunächst das Koordinatensystem einer
Drehung mit der Orthogonalmatrix  der Eigenvektoren von
der Eigenvektoren von  unterworfen wird, so daß die Form
unterworfen wird, so daß die Form
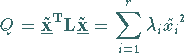 |
(4.136) |
entsteht, in der 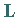 die Diagonalmatrix von
die Diagonalmatrix von  ist.
Daran schließt sich eine Dehnung mit der Diagonalmatrix
ist.
Daran schließt sich eine Dehnung mit der Diagonalmatrix 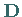 an, deren
Diagonalelemente
an, deren
Diagonalelemente 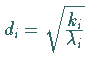 lauten.
Die Gesamtransformation wird dann durch
lauten.
Die Gesamtransformation wird dann durch
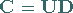 |
(4.137) |
beschrieben, und man erhält:
Hinweis: Die Hauptachsentransformation spielt eine wesentliche
Rolle bei der Klassifizierung von Kurven 2. Ordnung
und Flächen 2. Ordnung.
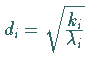 lauten.
Die Gesamtransformation wird dann durch
lauten.
Die Gesamtransformation wird dann durch