Zurückblättern Weiterblättern Übergeordnetes Thema Sachgebiet Hauptinhaltsverzeichnis Stichwortverzeichnis Hilfeseiten        


Hauptachsentransformation, Ähnlichkeitstransformation

Zu jeder reellen symmetrischen Matrix gibt es eine orthogonale Matrix und eine Diagonalmatrix 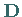mit
(4.128)

Dabei sind die Diagonalelemente von 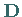die Eigenwerte von , und die Spalten von sind die dazugehörigen normierten Eigenvektoren. Aus der Gleichung (4.128) folgt unmittelbar
(4.129)

Man bezeichnet diese Gleichung als Hauptachsentransformation . Auf diese Weise wird in die Diagonalform überführt.
Wird die quadratische Matrix mit Hilfe der regulären quadratischen Matrix 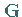nach der Vorschrift
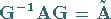(4.130)

transformiert, dann spricht man von einer Ähnlichkeitstransformation . Die Matrizen und 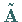heißen ähnlich, und es gilt:
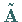1. Die Matrizen und haben dieselben Eigenwerte, d.h., bei einer Ähnlichkeitstransformation ändern sich die Eigenwerte nicht.
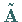2. Ist symmetrisch, dann ist auch symmetrisch, falls 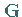orthogonal ist:

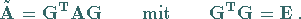(4.131)


Die Beziehung (4.131) heißt orthogonale Ähnlichkeitstransformation . Bei ihr bleiben Eigenwerte und Symmetrie erhalten. In diesem Zusammenhang besagt (4.129), daß eine symmetrische Matrix orthogonal ähnlich auf die reelle Diagonalform 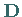transformiert werden kann.