|
|
|
|
| (4.126) |
3. Matrix mit p-fachem Eigenwert:
Zu einem ![]() -fachen Eigenwert
-fachen Eigenwert ![]() existieren
existieren ![]() linear unabhängige Eigenvektoren
linear unabhängige Eigenvektoren
![]() Wegen (4.124) sind auch alle nichttrivialen Linearkombinationen
Eigenvektoren zu
Wegen (4.124) sind auch alle nichttrivialen Linearkombinationen
Eigenvektoren zu ![]() .
Davon können
.
Davon können ![]() mit Hilfe des GRAM-SCHMIDTschen Orthogonalisierungsverfahrens
ausgewählt werden, die orthogonal sind.
Insgesamt gilt: Die Matrix
mit Hilfe des GRAM-SCHMIDTschen Orthogonalisierungsverfahrens
ausgewählt werden, die orthogonal sind.
Insgesamt gilt: Die Matrix ![]() besitzt genau
besitzt genau ![]() reelle orthogonale
Eigenvektoren.
reelle orthogonale
Eigenvektoren.
| Beispiel | |
|
| |
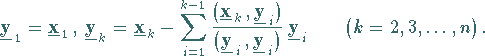 |
(4.127) |
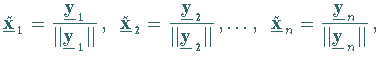 wobei mit
wobei mit 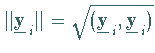 die EUKLIDische
Norm des Vektors
die EUKLIDische
Norm des Vektors | Beispiel | |
|
| |
|
|
|