Allgemeines Eigenwertproblem
und 
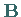seien zwei quadratische Matrizen vom Typ 
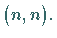Ihre Elemente können reelle oder komplexe Zahlen sein.
Die Aufgabe, Zahlen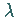 
und zugehörige Vektoren
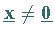mit
 |
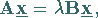(4.123) |
zu bestimmen, wird als allgemeines Eigenwertproblem bezeichnet.
Die Zahl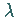
heißt Eigenwert , der Vektor 
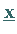Eigenvektor .
Ein Eigenvektor ist lediglich bis auf einen Faktor bestimmt, da mit
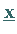auch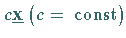 
Eigenvektor zu
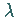ist.
Der Spezialfall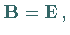 
wobei E eine 
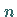-reihige Einheitsmatrix
ist, d.h.
 |
(4.124) |
wird als spezielles Eigenwertproblem bezeichnet.
Dieses tritt in vielen Anwendungen auf, vorwiegend mit symmetrischer Matrix
,
und wird im folgenden ausführlich dargestellt.
Bezüglich des allgemeinen Eigenwertproblems muß auf die Spezialliteratur verwiesen
werden (s. Lit. 4.1).
