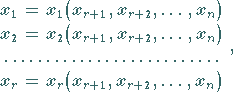Lösbarkeit eines linearen Gleichungssystems
Ein lineares Gleichungssystem heißt lösbar, wenn wenigstens ein Vektor
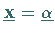 existiert, der
(4.107a) zu einer Identität macht.
Anderenfalls heißt das System unlösbar.
existiert, der
(4.107a) zu einer Identität macht.
Anderenfalls heißt das System unlösbar.
Das Lösungsverhalten hängt vom Rang der erweiterten Koeffizientenmatrix
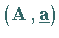 ab, die durch Hinzufügen der Komponenten des
Vektors
ab, die durch Hinzufügen der Komponenten des
Vektors 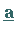 als
als 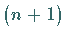 -te Spalte zur Matrix
-te Spalte zur Matrix  entsteht.
entsteht.
Im Folgenden wird die Lösbarkeit inhomogenerund
homogener Systemebetrachtet.
1. Allgemeine Regel für das inhomogene System:Das inhomogene System 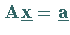 ist genau dann
lösbar, wenn
ist genau dann
lösbar, wenn
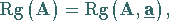 |
(4.108a) |
ist.
Für 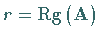 gilt die folgende Fallunterscheidung:
gilt die folgende Fallunterscheidung:
 |
(4.108b) |
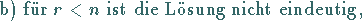 |
(4.108c) |
d.h., 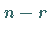 Unbekannte können als Parameter frei gewählt werden.
Unbekannte können als Parameter frei gewählt werden.
2. Triviale Lösung und Fundamentalsystem des homogenen Systems:
a) Das homogene Gleichungssystem 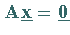 besitzt stets die sogenannte triviale Lösung
besitzt stets die sogenannte triviale Lösung
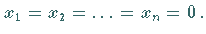
b) Besitzt es eine nichttriviale Lösung
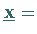
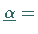
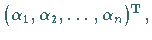 d.h.
d.h.
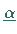
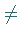
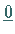 ,
dann ist auch
,
dann ist auch
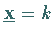
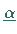 mit
mit 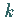 beliebig reell eine Lösung des homogenen Gleichungssystems.
Besitzt es
beliebig reell eine Lösung des homogenen Gleichungssystems.
Besitzt es 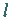 nichttriviale, linear unabhängige Lösungen
nichttriviale, linear unabhängige Lösungen
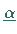
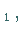
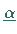
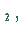 ...,
...,
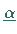
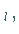 dann bilden diese ein sogenanntes
Fundamentalsystem, und die allgemeine Lösung des homogenen linearen
Gleichungssystems ist von der Form
dann bilden diese ein sogenanntes
Fundamentalsystem, und die allgemeine Lösung des homogenen linearen
Gleichungssystems ist von der Form
 |
(4.109) |
Gilt für den Rang der Koeffizientenmatrix  des homogenen Gleichungssystems
des homogenen Gleichungssystems
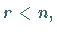 wobei
wobei 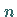 die Anzahl der Unbekannten ist, dann besitzt das homogene
Gleichungssystem ein Fundamentalsystem von Lösungen.
Im Falle
die Anzahl der Unbekannten ist, dann besitzt das homogene
Gleichungssystem ein Fundamentalsystem von Lösungen.
Im Falle  hat das homogene System nur die Triviallösung.
hat das homogene System nur die Triviallösung.
Zur Bestimmung eines Fundamentalsystems im Falle 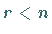 können
können 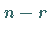 Unbekannte
als freie Parameter gewählt werden, und zwar derart, daß sich die übrigen
Unbekannten durch diese ausdrücken lassen, d.h., die entsprechende
Unbekannte
als freie Parameter gewählt werden, und zwar derart, daß sich die übrigen
Unbekannten durch diese ausdrücken lassen, d.h., die entsprechende 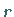 -reihige
Unterdeterminante darf nicht Null sein.
Man kann das durch Umordnen der Gleichungen und Unbekannten erreichen.
Erhält man z.B.
-reihige
Unterdeterminante darf nicht Null sein.
Man kann das durch Umordnen der Gleichungen und Unbekannten erreichen.
Erhält man z.B.
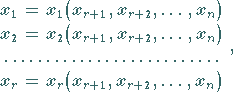 |
(4.110) |
dann ergeben sich die Fundamentallösungen z.B. durch die folgende Wahl der freien
Parameter:
 |
(4.111) |
![]() gilt die folgende Fallunterscheidung:
gilt die folgende Fallunterscheidung:
![]() Unbekannte können als Parameter frei gewählt werden.
Unbekannte können als Parameter frei gewählt werden.
![]() besitzt stets die sogenannte triviale Lösung
besitzt stets die sogenannte triviale Lösung
![]()
![]()
![]()
![]() d.h.
d.h.
![]()
![]()
![]() ,
dann ist auch
,
dann ist auch
![]()
![]() mit
mit ![]() beliebig reell eine Lösung des homogenen Gleichungssystems.
Besitzt es
beliebig reell eine Lösung des homogenen Gleichungssystems.
Besitzt es ![]() nichttriviale, linear unabhängige Lösungen
nichttriviale, linear unabhängige Lösungen
![]()
![]()
![]()
![]() ...,
...,
![]()
![]() dann bilden diese ein sogenanntes
Fundamentalsystem, und die allgemeine Lösung des homogenen linearen
Gleichungssystems ist von der Form
dann bilden diese ein sogenanntes
Fundamentalsystem, und die allgemeine Lösung des homogenen linearen
Gleichungssystems ist von der Form