Vektorielle Multiplikation
Die Vektorielle Multiplikation ist eine Operation, die zum Vektorprodukt zweier
Vektoren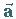 
und 
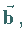auch Kreuzprodukt genannt, führt.
Dieses ergibt einen Vektor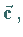 
der auf
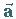und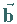 
senkrecht
steht, derart, daß die Vektoren 
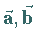und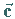 
ein
Rechtssystem bilden.
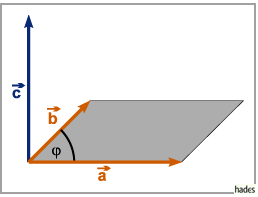
Vorausgesetzt, die Anfangspunkte der drei Vektoren sind in einem Punkt zusammengeführt,
dann ist das der Fall, wenn ein Beobachter, der auf die durch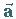
und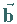
aufgespannte Ebene und gleichzeitig in die Richtung von
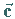blickt, den Vektor
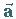durch die kürzeste Drehung im Uhrzeigersinn nach
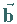überführen
kann.
Rechte-Hand-Regel: Die Vektoren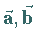
und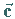
haben
dann die gleiche Orientierung, wie Daumen, Zeigefinger und Mittelfinger der rechten Hand
( Rechte-Hand-Regel ).
Quantitativ liefert das Vektorprodukt
 |
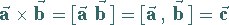(3.271a) |
einen Vektor der Länge
 |
(3.271b) |
wobei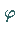 
der zwischen
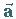und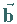
eingeschlossene Winkel ist.
Zahlenmäßig ist die Länge von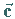
gleich dem Flächeninhalt des von
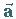und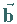
aufgespannten Parallelogramms.
