Zurückblättern Weiterblättern Übergeordnetes Thema Sachgebiet Hauptinhaltsverzeichnis Stichwortverzeichnis Hilfeseiten        

6. Grundaufgabe WWS

Gegeben: 2 Winkel und die einem Winkel gegenüberliegende Seite, z.B. 
Bedingungen: Siehe Fallunterscheidung.



Lösung: Gesucht beliebige fehlende Größe .
(3.226)

2 Werte sind möglich. Es sei spitz und stumpf.
Fallunterscheidung:
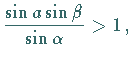  • d.h. 0 Lösungen.
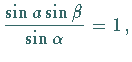  • d.h. 1 Lösung
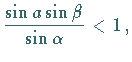  • d.h. weitere Fallunterscheidungen sind notwendig:

    • 3.1.  Weitere Fallunterscheidung:
    3.1.1.  d.h. 1 Lösung .
    3.1.2.  d.h. 1 Lösung .
    3.2.  Weitere Fallunterscheidung:
    3.2.1. , d.h. 2 Lösungen .
    3.2.2. , d.h. 0 Lösungen.
    Fortführung: Weitere Berechnung mit einer Seite oder 2 Seiten .


    1. Weg: Zerlegung des vorliegenden schiefwinklig sphärischen Dreiecks in zwei rechtwinklig sphärische Dreiecke, wobei die Seiten und auftreten.



    Dazu wird von das sphärische Lot auf bis gefällt.
    (3.227a)

    (3.227b)

    (3.227c)

    (3.227d)

    (3.227e)

    (3.227f)


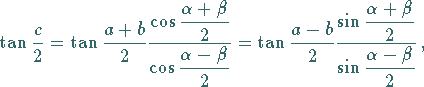    2. Weg: Mit Hilfe der NEPERschen Gleichungen (3.202b) und (3.202d) ergibt sich:
    (3.228a)

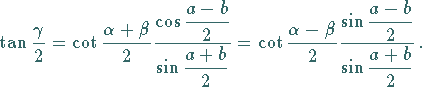    (3.228b)


    Probe: Doppelte Berechnung von

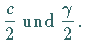
    Beispiel A Dreiseitige Pyramide

    Eine dreiseitige Pyramide hat die Grundfläche und die Spitze



    Die Seitenflächen und schneiden sich unter und unter und und unter . Wie groß sind die Winkel, unter denen sich je zwei der Kanten und schneiden?
    Lösung: Aus einer Kugelfläche um die Spitze der Pyramide schneidet das Dreikant ein sphärisches Dreieck mit den Seiten aus. Die Winkel zwischen den Seitenflächen sind die Winkel des sphärischen Dreiecks, die gesuchten Winkel zwischen den Kanten sind seine Seiten. Die Bestimmung der Winkel entspricht der 2. Grundaufgabe. Die 2. Lösung liefert:


    Beispiel B Funkpeilung

    Durch Funkpeilung von zwei festen Stationen und wurden die Azimute und der von einem Schiff ausgesandten Funkwellen gepeilt.



    Gesucht sind die geographischen Koordinaten des Standortes des Schiffes. Die in der Nautik unter dem Namen Fremdpeilung bekannte Aufgabe stellt einen Vorwärtseinschnitt auf der Kugel dar und wird ähnlich dem Vorwärtseinschnitt in der Ebene gelöst.

    1. Berechnung im Dreieck : Im Dreieck sind die Seiten und der Winkel gegeben. Die Berechnung der Winkel und der Strecke erfolgt gemäß 3. Grundaufgabe.

    2. Berechnung im Dreieck : Da sind in die Seite und die anliegenden Winkel und bekannt. Berechnung der Seiten und gemäß 4. Grundaufgabe, 3. Lösung. Die Koordinaten des Punktes sind aus dem Azimut und der Entfernung gegen oder , also doppelt berechenbar.

    3. Berechnung im Dreieck : Im Dreieck sind die zwei Seiten und der eingeschlossene Winkel gegeben.
    Nach der 3. Grundaufgabe, 1. Lösung, werden die Seiten und der Winkel berechnet. Zur Kontrolle werden im Dreieck ein zweites Mal und der Winkel berechnet. Damit sind die Länge und die Breite des Punktes bekannt.