Einfache Variationsaufgabe und Extremale
Als einfache Variationsaufgabe soll die folgende Aufgabe bezeichnet werden:
Es sind Extremwerte von Integralausdrücken der Form
 |
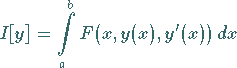(10.11) |
zu bestimmen, wenn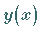 
alle zweimal stetig differenzierbaren Funktionen, die den
Randbedingungen 
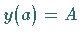und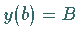 
genügen, durchläuft.
Die Werte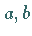 
und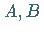 
sowie die Funktion 
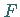sind gegeben.
Der Integralausdruck (10.11) ist ein Beispiel für ein sogenanntes
Funktional , das dadurch gekennzeichnet ist, daß es jeder Funktion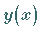
aus
einer bestimmten Funktionenklasse eine reelle Zahl zuordnet.
Nimmt das Funktional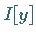 
von (10.11) z.B. für die Funktion 
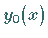ein
relatives Maximum an, dann gilt
 |
(10.12) |
beim Vergleiche mit allen anderen zweimal stetig differenzierbaren Funktionen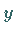 
,
die
den Randbedingungen genügen.
Die Kurve 
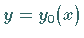wird als Extremale bezeichnet.
Manchmal werden auch alle Lösungen der EULERschen Differentialgleichung der
Variationsrechnung als Extremalen bezeichnet.
