Abbildungen
Eine Abbildung (oder Funktion) 
von einer Menge 
in eine Menge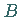 
(Bezeichnung 
)
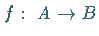ist eine Zuordnungsvorschrift, die jedem
Element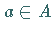 
eindeutig ein Element 
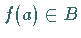zuordnet.
Man kann eine Abbildung
als zweistellige Relation zwischen
und
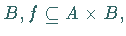auffassen: 
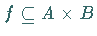heißt Abbildung von
nach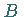 
falls gilt:
 |
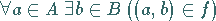(5.82) |
und
 |
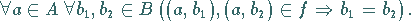(5.83) |
Die Funktion
heißt eineindeutig (oder injektiv ), falls zusätzlich
gilt:
 |
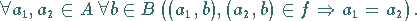(5.84) |
Während bei einer Abbildung nur verlangt wird, daß jedes Original nur ein Bild hat,
bedeutet Injektivität, daß auch jedes Bild nur ein Original besitzt.
Die Funktion
heißt Abbildung von
auf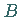
(oder surjektiv ), falls
gilt:
 |
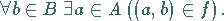(5.85) |
Eine injektive und surjektive Abbildung heißt bijektiv .
Für bijektive Abbildungen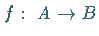
ist die inverse Relation eine Abbildung
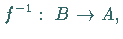die sogenannte Umkehrabbildung von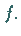 
Das Relationenprodukt, auf Abbildungen angewandt, charakterisiert die
Hintereinanderausführung von Abbildungen:
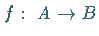Sind
und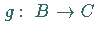 
Abbildungen, so ist 
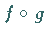eine Abbildung von
nach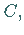 
und es gilt
 |
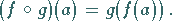(5.86) |
Man beachte die Reihenfolge von
und 
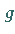in dieser Gleichung (unterschiedliche
Handhabung in der Literatur!).
