|
|
|
|
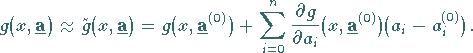 |
(19.187) |
2. Lösung der linearen Ausgleichsaufgabe
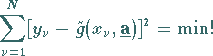 |
(19.188) |
mit Hilfe des Normalgleichungssystems
gegeben.
Die Matrix ![]() wird analog zu
wird analog zu ![]() in (19.179b) gebildet, indem man
in (19.179b) gebildet, indem man
![]() durch
durch
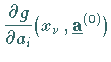
![]() ersetzt.
ersetzt.
3. Berechnung einer neuen Näherung durch
| (19.191) |
wobei ![]() ein Schrittweitenparameter ist.
ein Schrittweitenparameter ist.
Durch Wiederholung der Schritte 2 und 3 mit ![]() an Stelle von
an Stelle von ![]() usw.
erhält man für die gesuchten Parameter Folgen von Näherungswerten, deren Konvergenz
sehr stark von der Güte der Startnäherung abhängt.
Mit Hilfe des Schrittweitenparameters
usw.
erhält man für die gesuchten Parameter Folgen von Näherungswerten, deren Konvergenz
sehr stark von der Güte der Startnäherung abhängt.
Mit Hilfe des Schrittweitenparameters ![]() läßt sich aber zunächst eine
Verkleinerung der Fehlerquadratsumme erzielen.
läßt sich aber zunächst eine
Verkleinerung der Fehlerquadratsumme erzielen.
|
|
|