In Matrizenschreibweise haben die Normalgleichungen (19.177) und die
Fehlerquadratsumme (19.176) die folgende übersichtliche Form:
 |
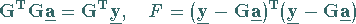(19.179a) |
mit
 |
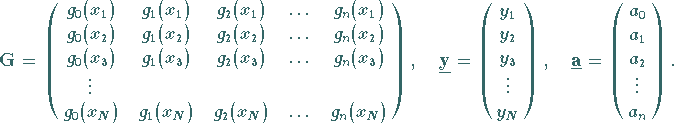(19.179b) |
Würde man an Stelle der Forderung, die Fehlerquadratsumme zu minimieren, in den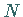 
Punkten 
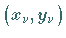die Interpolationsforderung stellen, dann ergäbe sich das
Gleichungssystem
 |
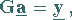(19.180) |
ein überbestimmtes lineares Gleichungssystem im Fall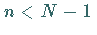 
,
das in der Regel
keine Lösung hat.
Durch Multiplikation mit 
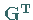erhält man aus (19.180) das
Normalgleichungssystem (19.177) bzw. (19.179a).
Aus numerischer Sicht ist es jedoch günstiger, zur Lösung von Ausgleichsaufgaben auf
(19.180) das HOUSEHOLDER-Verfahren anzuwenden, das eine
Lösung im Sinne der minimalen Fehlerquadratsumme (19.176) liefert.
