Bemerkungen
1. Sind die Ansatzkoeffizienten gemäß (19.155) bestimmt
worden, dann stellt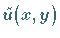 
aus (19.147) eine explizite
Näherungslösung dar, deren Werte für beliebige Punkte 
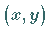aus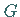 
berechnet werden können.
2. Muß das Integrationsgebiet mit einem beliebigen, unregelmäßigen
Dreiecksnetz überzogen werden, dann ist es zweckmäßig, sogenannte
Dreieckskoordinaten (auch baryzentrische Koordinaten genannt) einzuführen.
Dadurch ist die Lage eines Punktes bezüglich des Dreiecksnetzes leicht feststellbar,
und die Berechnung der mehrdimensionalen Integrale analog zu (19.152) wird
vereinfacht, weil jedes beliebige Dreieck besonders einfach auf ein Einheitsdreieck
transformiert werden kann.
3. Soll die Genauigkeit der Näherungsfunktion erhöht oder ihre
Differenzierbarkeit gewährleistet werden, dann muß man zu stückweise quadratischen
oder stückweise kubischen Ansatzfunktionen übergehen (s. z. B. Lit 19.25).
4. Bei der Lösung praktischer Probleme entstehen Aufgaben sehr
großer Dimension.
Deshalb wurden viele spezielle Verfahren entwickelt, z.B. auch für eine automatische
Triangulierung und für eine günstige Numerierung der Elemente (davon hängt die
Struktur der Gleichungssysteme ab, die gelöst werden müssen).
Eine ausführliche Darstellung der FEM s. Lit. 19.13, 19.9, 19.26.
