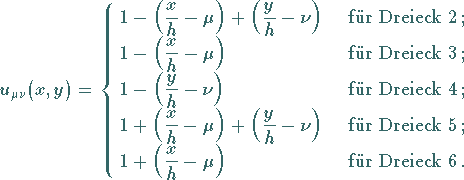Ansatz
Für die gesuchte Funktion 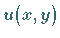 wird in jedem Dreieck ein Ansatz gemacht.
Ein Dreieck mit zugehörigem Ansatz wird als finites Element bezeichnet.
Dafür eignen sich Polynome in
wird in jedem Dreieck ein Ansatz gemacht.
Ein Dreieck mit zugehörigem Ansatz wird als finites Element bezeichnet.
Dafür eignen sich Polynome in 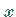 und
und 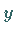 .
In vielen Fällen reicht der lineare Ansatz
.
In vielen Fällen reicht der lineare Ansatz
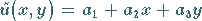 |
(19.146) |
aus.
Die Ansatzfunktionen müssen beim Übergang von einem Dreieck ins benachbarte zumindest
stetig sein, damit eine stetige Gesamtlösung entsteht.
Die Koeffizienten 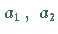 und
und 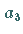 in (19.146) lassen sich eindeutig
durch die drei Funktionswerte
in (19.146) lassen sich eindeutig
durch die drei Funktionswerte 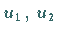 und
und 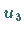 in den Eckpunkten des
zugehörigen Dreiecks ausdrücken.
Dadurch ist gleichzeitig der stetige Übergang in die benachbarten Dreiecke gesichert.
Der Ansatz (19.146) enthält damit als unbekannte Parameter die Näherungen
in den Eckpunkten des
zugehörigen Dreiecks ausdrücken.
Dadurch ist gleichzeitig der stetige Übergang in die benachbarten Dreiecke gesichert.
Der Ansatz (19.146) enthält damit als unbekannte Parameter die Näherungen
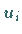 für die gesuchten Funktionswerte.
Als Ansatz, der im gesamten Gebiet
für die gesuchten Funktionswerte.
Als Ansatz, der im gesamten Gebiet 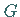 für die gesuchte Lösung
für die gesuchte Lösung 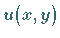 als Näherung
verwendet wird, wählt man
als Näherung
verwendet wird, wählt man
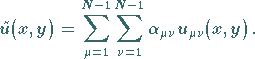 |
(19.147) |
Die Koeffizienten  sind noch geeignet zu bestimmen.
Für die Funktionen
sind noch geeignet zu bestimmen.
Für die Funktionen 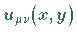 soll gelten:
Sie stellen über jedem Dreieck von
soll gelten:
Sie stellen über jedem Dreieck von  eine lineare Funktion gemäß
(19.146) dar und erfüllen die folgenden Bedingungen:
eine lineare Funktion gemäß
(19.146) dar und erfüllen die folgenden Bedingungen:
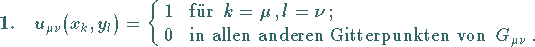 |
(19.148a) |
 |
(19.148b) |
Die Darstellung von 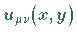 über
über  zeigt die folgende Abbildung:
zeigt die folgende Abbildung:
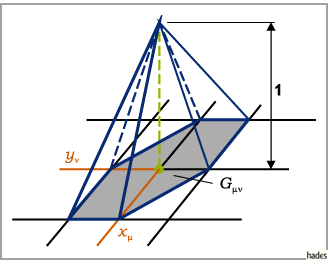
Die Berechnung von 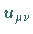 über
über  ,
d.h. über den Dreiecken 1 bis 6
in der Abbildung, soll für das Dreieck 1 gezeigt werden:
,
d.h. über den Dreiecken 1 bis 6
in der Abbildung, soll für das Dreieck 1 gezeigt werden:
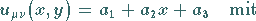 |
(19.149a) |
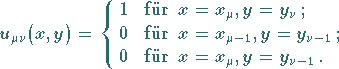 |
(19.149b) |
Aus (19.149b) folgt 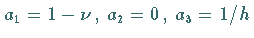 ,
und man erhält für Dreieck 1:
,
und man erhält für Dreieck 1:
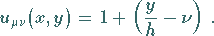 |
(19.149c) |
Analog berechnet man:
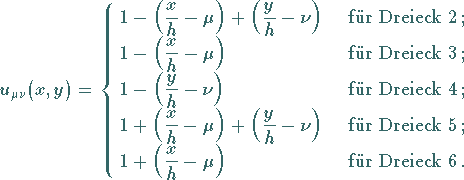 |
(19.150) |
![]() über
über ![]() zeigt die folgende Abbildung:
zeigt die folgende Abbildung: