|
|
|
|
häufig Meßwerte, also fehlerbehaftet.
In diesem Fall ist die Interpolationsforderung unzweckmäßig.
Man führt deshalb den kubischen Ausgleichsspline ein.
Er entsteht, wenn man beim kubischen Interpolationsspline die Interpolationsforderung durch
und 
bleibt erhalten, so daß sich
zur Bestimmung der Spline-Koeffizienten eine Extremwertaufgabe mit Nebenbedingungen in
Gleichungsform ergibt.
Die Lösung erfolgt mit Hilfe einer LAGRANGE-Funktion.
Einzelheiten s. Lit. 19.30, 19.31.
In (19.237) stellt 
einen
Glättungsparameter dar, der vorgegeben werden muß.
Für 
ergibt sich als Spezialfall der kubische Interpolationsspline, für
,,große`` 
erhält man eine glatte Näherungskurve, die dafür aber
die Meßpunkte nur ungenau wiedergibt, und für 
ergibt sich
schließlich als weiterer Spezialfall die Ausgleichsgerade.
Eine geeignete Wahl von
kann am Computer im Bildschirmdialog erfolgen.
Die Parameter 
in (19.237) stellen die
Standardabweichungen der Meßfehler dar, mit denen die Meßwerte
evtl. behaftet sind.
Bei den bisher betrachteten kubischen Interpolations- und Ausgleichssplines waren die
Abszissen der Interpolations- bzw. Meßpunkte identisch mit den Knoten der
Spline-Funktion.
Das hat zur Folge, daß bei großem 
der Spline aus einer sehr großen Anzahl
von kubischen Ansatzfunktionen (19.231) besteht.
Es liegt nahe, Anzahl und Lage der Knotenpunkte frei zu wählen, da man in der Praxis
meist mit wesentlich weniger Spline-Stücken auskommt.
Darüber hinaus ist es numerisch günstiger, an Stelle des Ansatzes (19.231)
Splines in der Form
 |
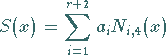(19.238) |
anzusetzen.
Dabei ist 
die Anzahl der frei gewählten Knoten, und mit 
werden die
sogenannten normalisierten 
-Splines ( Basis-Splines ) der Ordnung 4, d.h.
vom Polynomgrad 3, zum 
-ten Knoten bezeichnet.
Ausführungen dazu s. Lit. 19.4.
|
|
