Bestimmung der Spline-Koeffizienten
Für den kubischen Interpolationsspline 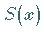 wird für
wird für 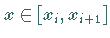 der Ansatz
der Ansatz
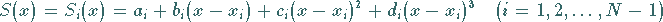 |
(19.231) |
gemacht.
Die Länge der Teilintervalle wird mit 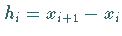 bezeichnet.
Zur Bestimmung der Ansatzkoeffizienten für den natürlichen Spline kann man wie folgt
vorgehen:
bezeichnet.
Zur Bestimmung der Ansatzkoeffizienten für den natürlichen Spline kann man wie folgt
vorgehen:
1. Aus der Interpolationsforderung folgt
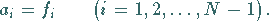 |
(19.232) |
Es ist zweckmäßig, den im Ansatz nicht auftretenden Koeffizienten 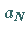 einzuführen und
einzuführen und 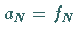 zu setzen.
zu setzen.
2. Die Stetigkeit von 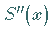 an den inneren Knoten führt zu
an den inneren Knoten führt zu
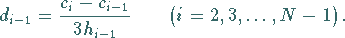 |
(19.233) |
Aus den natürlichen Randbedingungen folgt 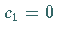 ,
und (19.233) gilt
auch für
,
und (19.233) gilt
auch für 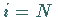 ,
wenn man
,
wenn man 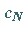 einführt und
einführt und 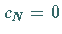 setzt.
setzt.
3. Die Stetigkeit von 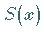 an den inneren Knoten führt zu
an den inneren Knoten führt zu
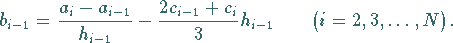 |
(19.234) |
4. Die Stetigkeit von 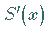 an den inneren Knoten ergibt
an den inneren Knoten ergibt
Wegen (19.232) ist die rechte Seite des linearen Gleichungssystems
(19.235) zur Bestimmung der Koeffizienten
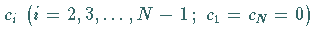 bekannt.
Die linke Seite hat folgende Gestalt:
bekannt.
Die linke Seite hat folgende Gestalt:
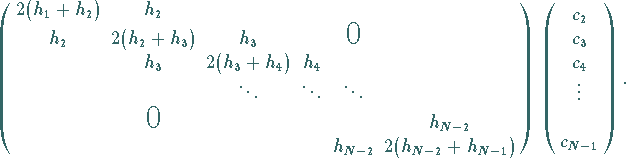 |
(19.236) |
Die Koeffizientenmatrix ist tridiagonal , so daß sich das Gleichungssystem
(19.235) durch LR-Zerlegung sehr einfach numerisch
lösen läßt.
Aus den Koeffizienten 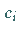 erhält man über (19.234) und (19.233) die
restlichen Koeffizienten.
erhält man über (19.234) und (19.233) die
restlichen Koeffizienten.