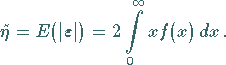Themen dieser Seite
Fehler der Einzelmessung einer Meßreihe
1. Wahrer und scheinbarer Fehler der Einzelmessung einer Meßreihe
1. Wahrer Fehler der Einzelmessung einer Meßreihe
wird die Abweichung des Meßergebnisses vom wahren Wert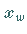 
genannt.
Da dieser meist unbekannt ist, bleibt auch der wahre Fehler 
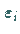der
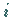-ten Messung mit dem Ergebnis 
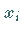unbekannt:
 |
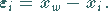(16.201a) |
2. Scheinbarer Fehler der Einzelmessung einer Meßreihe
wird die Abweichung des Meßergebnisses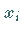
vom arithmetischen Mittelwert genannt:
 |
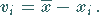(16.201b) |
2. Mittlerer quadratischer Fehler der Einzelmessung oder Standardabweichung
der Einzelmessung
Da der Erwartungswert der Summe der wahren Fehl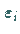er
und der Erwartungswert
der Summe der scheinbaren Fehler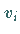 
von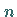 
Messungen einer Größe verschwindet,
werden die verschiedenen Fehler mit Hilfe der Fehlerquadratsummen berechnet:
 |
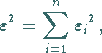(16.202a) |
 |
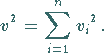(16.202b) |
Für die praktische Auswertung ist nur (16.202b) von Interesse, weil nur die
Werte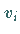
aus den Meßergebnissen ermittelt werden können.
Deshalb definiert man
 |
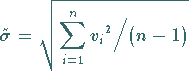(16.203) |
als mittleren quadratischen Fehler der Einzelmessung der Meßreihe.
Der Wert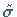 
ist ein Näherungswert für die Standardabweichung 
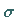der Fehlerverteilung.
Im Falle der Fehlernormalverteilung gilt für 
:
 |
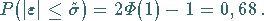(16.204) |
Das bedeutet: Die Wahrscheinlichkeit, daß der wahre Fehler betragsmäßig den
Wert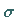
nicht übersteigt, beträgt ca. 68 %.
3. Wahrscheinlicher Fehler
Wahrscheinlicher Fehler ist die Bezeichnung für eine Zahl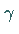 
,
für die gilt:
 |
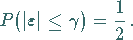(16.205) |
Das bedeutet: Die Wahrscheinlichkeit, daß der Fehler den Wert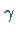 
nicht
übersteigt, beträgt in diesem Falle 50 %.
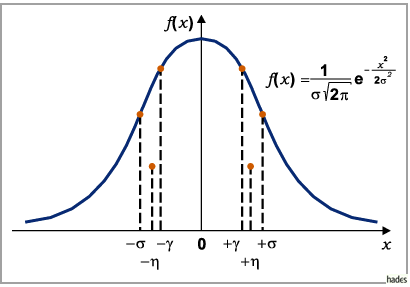
Die Abszissenwerte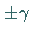 
teilen die linke und rechte Fläche unter der
Dichtefunktion in je zwei gleich große Hälften (s. Abbildung).
Im Falle der Fehlernormalverteilung besteht zwischen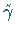 
und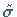
der Zusammenhang
 |
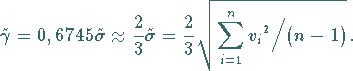(16.206) |
4. Mittlerer Fehler
Mittlerer Fehler ist die Bezeichnung für eine Zahl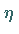 
,
die als Erwartungswert des
absoluten Betrages des Fehlers definiert wird:
 |
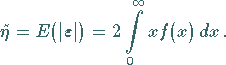(16.207) |
Im Falle der Fehlernormalverteilung ergibt sich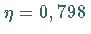 
.
Auf Grund der Beziehung
 |
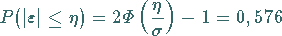(16.208) |
folgt daraus:
Die Wahrscheinlichkeit, daß der Fehler den Wert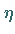 
nicht übersteigt, beträgt
ca. 57,6 %.
Bei den Abszissenwerten 
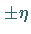liegen die Schwerpunkte der rechten bzw. linken Fläche
unter der Dichtefunktion (s. Abbildung).
Im Falle der Fehlernormalverteilung gilt
 |
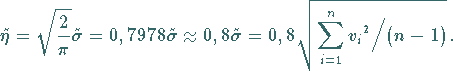(16.209) |
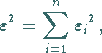
