Formeln für die Fourier-Koeffizienten
Da das Funktionensystem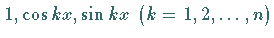 
bezüglich des
Intervalls 
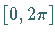und bezüglich der Gewichtsfunktion 
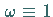orthogonal ist, erhält man durch Anwendung der Fehlerquadratmethode im stetigen Fall
gemäß (19.169) für die Ansatzkoeffizienten die Formeln
 |
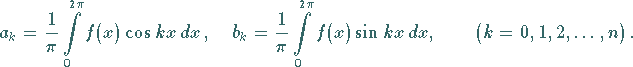(19.208) |
Die Koeffizienten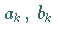 
,
die nach der Formel (19.208) berechnet
werden, heißen
FOURIER-Koeffizienten der periodischen Funktion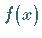 
.
Lassen sich die in (19.208) auftretenden Integrale nicht mehr elementar oder nur
mit großem Rechenaufwand integrieren oder ist die Funktion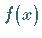
nur punktweise
bekannt, dann kann man die FOURIER-Koeffizienten näherungsweise durch numerische
Integration ermitteln.
Durch die Anwendung der Trapezformel mit den gleichabständigen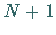 
Stützstellen
 |
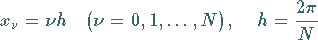(19.209) |
erhält man die Näherungsformeln
 |
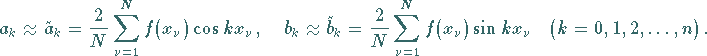(19.210) |
Im vorliegenden Fall periodischer Funktionen ist die Trapezformel in die sehr einfache
Rechteckregel übergegangen.
Diese ist hier von großer Genauigkeit, denn es gilt:
Ist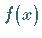
periodisch und 
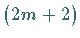-mal stetig differenzierbar, dann hat die Trapezformel
die Fehlerordnung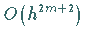 
.
