Stetige Aufgabe, Normalgleichungen
Eine Funktion 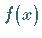 ist über dem Intervall
ist über dem Intervall 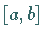 durch eine Funktion
durch eine Funktion 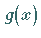 in dem
Sinne zu approximieren, daß der Ausdruck
in dem
Sinne zu approximieren, daß der Ausdruck
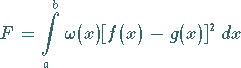 |
(19.166) |
minimal wird, und zwar in Abhängigkeit von den Parametern, die die Funktion 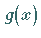 enthält.
Mit
enthält.
Mit 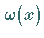 ist eine gegebene Gewichtsfunktion bezeichnet, für die
ist eine gegebene Gewichtsfunktion bezeichnet, für die
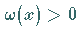 im Integrationsintervall gelten soll.
im Integrationsintervall gelten soll.
Macht man für die Näherungsfunktion 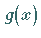 den Ansatz
den Ansatz
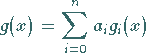 |
(19.167) |
mit geeigneten, linear unabhängigen Funktionen
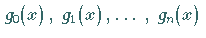 ,
dann führen die notwendigen Bedingungen
,
dann führen die notwendigen Bedingungen
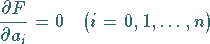 |
(19.168) |
für ein relatives Minimum von (19.166) auf das sogenannte
Normalgleichungssystem
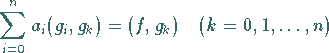 |
(19.169) |
zur Bestimmung der Ansatzkoeffizienten 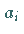 .
Dabei werden die Abkürzungen
.
Dabei werden die Abkürzungen
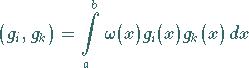 |
(19.170a) |
und
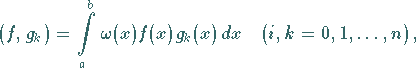 |
(19.170b) |
die auch als Skalarprodukte der betreffenden zwei Funktionen bezeichnet werden,
verwendet.
Das System der Normalgleichungen ist eindeutig lösbar, da für die Ansatzfunktionen
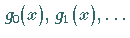 ,
,
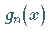 lineare Unabhängigkeit vorausgesetzt war.
Die Koeffizientenmatrix des Systems (19.169) ist symmetrisch, so daß zur
Lösung das CHOLESKY-Verfahren verwendet werden sollte.
lineare Unabhängigkeit vorausgesetzt war.
Die Koeffizientenmatrix des Systems (19.169) ist symmetrisch, so daß zur
Lösung das CHOLESKY-Verfahren verwendet werden sollte.
Die Ansatzkoeffizienten 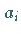 können direkt berechnet werden, ohne Lösung eines
Gleichungssystems, wenn das System der Ansatzfunktionen orthogonal ist, d.h. wenn
gilt:
können direkt berechnet werden, ohne Lösung eines
Gleichungssystems, wenn das System der Ansatzfunktionen orthogonal ist, d.h. wenn
gilt:
 |
(19.171) |
Darüber hinaus spricht man von einem orthonormierten System, wenn gilt:
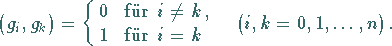 |
(19.172) |
Mit (19.172) vereinfachen sich die Normalgleichungen
(19.169) zu
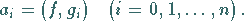 |
(19.173) |
Linear unabhängige Funktionensysteme können orthogonalisiert werden.
Aus den Potenzfunktionen 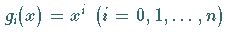 erhält man je nach
Wahl der Gewichtsfunktion und des Integrationsintervalls die folgenden
Orthogonalpolynome :
erhält man je nach
Wahl der Gewichtsfunktion und des Integrationsintervalls die folgenden
Orthogonalpolynome :
Tabelle Orthogonalpolynome
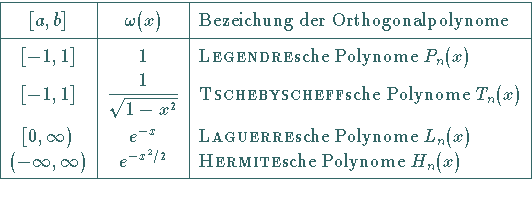 |
(19.174) |
Mit dieser Auswahl können die wichtigsten Anwendungsfälle berücksichtigt werden:
1. endliches Approximationsintervall,
2. einseitig unendliches Approximationsintervall, z.B. bei zeitabhängigen
Problemen,
3. zweiseitig unendliches Approximationsintervall, z.B. bei Strömungsproblemen.
Man beachte, daß jedes endliche Intervall 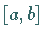 durch die Substitution
durch die Substitution
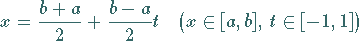 |
(19.175) |
auf das Intervall 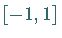 ,
für das viele Ansatzfunktionen definiert sind,
transformiert werden kann.
,
für das viele Ansatzfunktionen definiert sind,
transformiert werden kann.
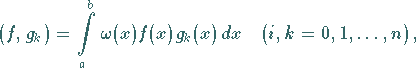
![]() ,
,
![]() lineare Unabhängigkeit vorausgesetzt war.
Die Koeffizientenmatrix des Systems (19.169) ist symmetrisch, so daß zur
Lösung das CHOLESKY-Verfahren verwendet werden sollte.
lineare Unabhängigkeit vorausgesetzt war.
Die Koeffizientenmatrix des Systems (19.169) ist symmetrisch, so daß zur
Lösung das CHOLESKY-Verfahren verwendet werden sollte.
![]() können direkt berechnet werden, ohne Lösung eines
Gleichungssystems, wenn das System der Ansatzfunktionen orthogonal ist, d.h. wenn
gilt:
können direkt berechnet werden, ohne Lösung eines
Gleichungssystems, wenn das System der Ansatzfunktionen orthogonal ist, d.h. wenn
gilt:
![]() erhält man je nach
Wahl der Gewichtsfunktion und des Integrationsintervalls die folgenden
Orthogonalpolynome :
erhält man je nach
Wahl der Gewichtsfunktion und des Integrationsintervalls die folgenden
Orthogonalpolynome :

![]() ,
für das viele Ansatzfunktionen definiert sind,
transformiert werden kann.
,
für das viele Ansatzfunktionen definiert sind,
transformiert werden kann.