|
|
|
|
(Vektorfeld) eine 
-mal stetig
differenzierbare Abbildung ist und 
oder eine offene Teilmenge des 
darstellt.
Im weiteren wird im
stets die
EUKLIDische Norm 
benutzt, d.h., für
beliebiges 
ist
.
Schreibt man die Abbildung 
in Komponenten als 
,
so ist
(17.1) das System aus den 
skalaren Differentialgleichungen
.
Die Sätze über die lokal eindeutige Lösbarkeit von
PICARD-LINDELÖF und
über die -malige Differenzierbarkeit nach den Anfangsbedingungen
(s. Lit. 17.6) garantieren, daß für jedes 
eine Zahl
,
eine Kugel
aus 
und eine Abbildung
existieren,
so daß gilt:
1. 
ist 
-mal stetig differenzierbar bezüglich
des ersten Arguments (Zeit) und -mal stetig differenzierbar bezüglich des zweiten
Arguments (Ortsvariable).
2. 
ist für jedes fixierte
eine lokal eindeutige Lösung von (17.1) auf dem Zeitintervall
mit Anfang 
zur Zeit 
,
d.h., es gilt
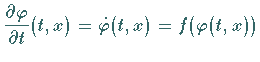für alle 
,
und jede
andere Lösung mit Anfang
zur Zeit 
stimmt für kleine Zeiten 
mit
überein.
Alle lokalen Lösungen von (17.1) seien eindeutig auf ganz 
fortsetzbar.
Dann gibt es zu jeder Differentialgleichung (17.1) eine Abbildung
mit folgenden Eigenschaften:
1. 
.
2. 
.
3. 
ist bezüglich des ersten Arguments -mal und
bezüglich des zweiten Arguments -mal stetig differenzierbar.
4. 
ist für jedes fixierte 
eine Lösung von
(17.1) auf ganz 
.
Der zu (17.1) gehörige 
-glatte Fluß läßt sich dann durch die
Beziehung 
definieren.
Die Bewegungen 
eines Flusses von (17.1)
heißen Integralkurven .
In dem folgenden Beispiel wird das LORENZ-System betrachtet.
| Beispiel | |
und 
Parameter.
Dem LORENZ-System entspricht ein 
-Fluß in 
.
|
|
