Satz von Picard-Lindelöf
Es werde die Differentialgleichung
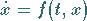 |
(12.68) |
mit einer stetigen Abbildung 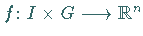 betrachtet, wobei
betrachtet, wobei 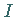 ein offenes Intervall aus
ein offenes Intervall aus 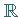 und
und 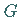 eine offene Teilmenge aus
eine offene Teilmenge aus
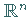 sind.
Die Abbildung
sind.
Die Abbildung  genüge bezüglich
genüge bezüglich 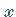 einer LIPSCHITZ-Bedingung,
d.h., es gibt eine positive Konstante
einer LIPSCHITZ-Bedingung,
d.h., es gibt eine positive Konstante 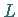 mit
mit
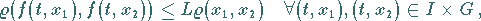 |
(12.69) |
wobei 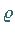 die euklidische Metrik in
die euklidische Metrik in  bezeichnet
(unter Verwendung der Norm, gilt die Beziehung (12.79)
bezeichnet
(unter Verwendung der Norm, gilt die Beziehung (12.79)
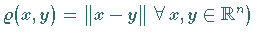 .
Sei
.
Sei 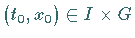 ein beliebiger Punkt.
Dann gibt es solche Zahlen
ein beliebiger Punkt.
Dann gibt es solche Zahlen 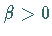 und
und 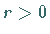 so, daß die Menge
so, daß die Menge
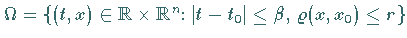 in
in 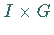 liegt.
Seien
liegt.
Seien 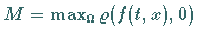 und
und
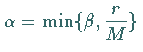 .
Dann existiert eine Zahl
.
Dann existiert eine Zahl 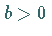 ,
so daß für jedes
,
so daß für jedes 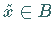 mit
mit
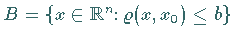 das Anfangswertproblem
das Anfangswertproblem
 |
(12.70) |
genau eine (lokale) Lösung 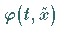 besitzt, d.h.
besitzt, d.h.
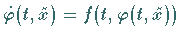 für
für
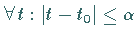 und
und 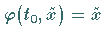 .
Die Lösung dieses Anfangswertproblems ist äquivalent zur Lösung der
Integralgleichung
.
Die Lösung dieses Anfangswertproblems ist äquivalent zur Lösung der
Integralgleichung
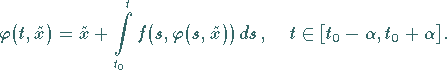 |
(12.71) |
Bezeichnet jetzt  die abgeschlossene Kugel
die abgeschlossene Kugel
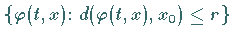 des in der Metrik
des in der Metrik
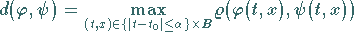 |
(12.72) |
vollständigen metrischen Raumes
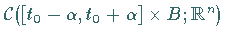 ,
dann ist
,
dann ist  mit der
induzierten Metrik selbst ein vollständiger metrischer Raum.
Ist
mit der
induzierten Metrik selbst ein vollständiger metrischer Raum.
Ist 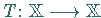 der durch
der durch
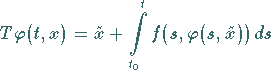 |
(12.73) |
definierte Operator, dann ergibt sich die Lösung der Integralgleichung (12.71)
als eindeutiger Fixpunkt des Operators 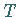 ,
der sogar iterativ erzeugt werden kann.
,
der sogar iterativ erzeugt werden kann.
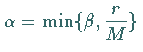 .
Dann existiert eine Zahl
.
Dann existiert eine Zahl 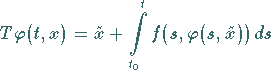
![]() ,
der sogar iterativ erzeugt werden kann.
,
der sogar iterativ erzeugt werden kann.